[G] Question 1: Easy Geometry
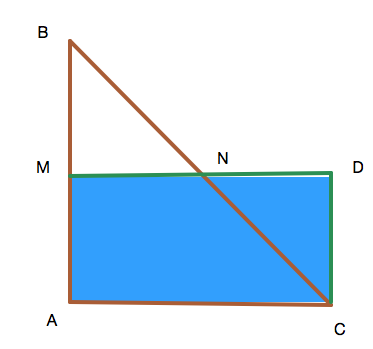 ABC is a right angle triangle with angle
B
A
C
=
9
0
∘
.
ABC is a right angle triangle with angle
B
A
C
=
9
0
∘
.
Let M and N be the midpoints of BA and BC respectively.
Let D be a point on MN extended such that CD//AB
The ratio of the area of quadrilateral AMDC to the area of triangle ABC is
b
a
where a and b are coprime integers.
Find a+b.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
21 solutions
area of the triangle is .5 AC AB & area of the rectangle is AC MN. Since, M is the midpoint of AB, so, AM=.5 AB, which means the rectangle and the the triangle have equal area.
please follow me thanks
length of CD=length of BM and length of BN=length of CN, angle BMN= angle CND so triangles are identical in dimensions, therefore the relation is 1 : 1 but the answer could be anything and doesn't have to be 2 , a better question would be: the area of the triangle is say 10, find the area of the rectangle for which the answer would of course be 10.
It never says the area in the first case, when they specify the ratio it could mean the perimeter not the area, which in this case is different from the triangle and the square areas and of course the ratio could be 1 to 1 or 2 to 2 in which case the answer also could be anything from 2 to 4 to 6 and so on.
Log in to reply
Are you on drugs?
"The ratio of the area of quadrilateral AMDC to the area of triangle ABC is (a/b) where a and b are coprime integers. Find a+b."
The area of both is: [AC(AB)]/2 :. a=b, but a & b are coprimes, and the only solution for a=b; a | b is 1.
(2,2) has the prime 2 in common, etc. Other wise every prime would be a coprime of itself.
yeah!! that's how I'm stucked for a second ...
area of triangle=(ABXAC)/2 =(ABXAB)/2 as AB=AC Now Area of rectangle=AMXAC =(AB/2)XAB as AM=AB/2 and AB=AC Then Area of rectangle=(ABXAB)/2 Now as per the que {(ABXAB)/2}/{(ABXAB)/2}=a/b Then a/b=1/1 a=1 and b=1 then a+b=2
I can't assume that BA=AC since the question didn't tell me that. But you can still get the answer that way anyway.
Let BM=MA=c, MN=ND=d.
So BA=2c and AC=MD=2d.
A r e a o f q u a d r i l a t e r a l A M D C = c × 2 d = 2 c d A r e a o f t r i a n g l e A B C = 2 1 ( 2 c × 2 d ) = 2 1 ( 4 c d ) = 2 c d A B C : A M D C = a : b = 2 c d : 2 c d = 1 : 1 S o a + b = 2
Thank you for the answer.
I must say question is nicely framed. the answer is 2 cause area of triangle is 1/2 b h and that of square is l b from the figure it's clear that both areas are same ,polygon has 1 side equal to half of triangle makes it's final area equal to 1/2 b*h so ratio is 1:1
but hows it 2
area are equal so it is 1:1 therefore 1+1=2
MN is half the measure of AC (Midline Theorem). Since segments MN and ND when combined is equal to segment AC, then ND is also half the measure of AC, thus MN and ND are congruent.
M and N are the midpoints of segments BA and BC respectively, thus BM is congruent to BA and BN is congruent to BC. MA is obviously congruent to DC, so DC is also congruent to BM. Here we could conclude that Triangles CDN and BMN are congruent.
Analyzing the figure carefully, we can say that the areas of the quadrilateral and bigger triangle are equal since the two smaller triangles are congruent . The ratio is 1:1 and the value of a+b is 2.
The areas of the two shapes are obviously the same, but if it isn't clear from looking, here's some proof:
Imagine moving △ N D C (part of the rectangle) on top of △ N M B (part of the actual triangle. If you did this, the two shapes would be completely congruent, and the areas would not have changed. So basically, to prove the areas of the two shapes are the same, we have to prove that △ N D C = △ N M B . Well M N = N D since N is the midpoint of M D . That's one side. Also, B N = N C since N is also the midpoint of B C . That's 2 corresponding sides. Finally, ∠ M N B = ∠ D N C since they are vertical angles. So now we have 2 equal pairs of corresponding sides, with 1 angle in-between. This looks to me like the perfect candidate for the SAS congruency postulate! So we've proved that the 2 triangles have equal area, and therefore the rectangle and the triangle have the exact same area! That means that the simplified ratio would be 1:1. The only 1:1 ratio with coprime integers in it is 1:1, which means that a = 1 and b = 1 . With this information we can now solve the problem: 1 + 1 = 2 . Easy!
let l is length AC b is AB area of triangle is .5 l b area of rectangle is l 0.5 b AM =0.5AB ratio is 1/1 ans 2
Write a solution. triangle BMN and CDN are congruent and the remaining area is common in both the figures thus ratio 1:1 and answer 1+1=2
Proove BMN and CDN are the same triangles by SAA( side angle angle). This will show that the ratio is 1:1 and 1+1=2
Area of ABC = 1/2 x AB x AC = AM x AC (since AM = 1/2 x AB). Area of AMDC = AM x AC. => a/b = AM x AC / AM x AC = 1/1. So a + b = 1 +1 = 2.
here answer can't be determine correctly in numerical value, but it will be double of area of rectangle or double of area of triangle (as both has equal area)
In the given information, the statement that a and b are coprime integers is superfluous. This is not required to say that a+b = 2.
AM=AB/2 Area of ACDM=AC×AB/2=Area of ABC=1/2×AB×AC.
Ratio=1:1. Answer= 1+1=2
if ratio is 1;1,then it is posiible that a=2,b=2 so nowa;b=1;1 but a+b=4
if you move /\ NCD to /\BNM they are exactly the same
Area of both rectangle and triangle are equal. since the a & b are coprime no so the ration must be 1:1. then a+b=2
first time i was confused that how can give ans. but i was known the ans. easy question.
area of both rectangle and triangle are equal. since the a & b are coprime no so the ration must be 1:1. then a+b=2