Galvagni figure numbers
The Galvagni figure for a shape is the smallest figure that can be tiled by that shape in more than one way.
The Galvagni figure number for a shape is the number of copies that fit inside.
For example, the Galvagni figure for a straight tromino is a square and the figure number is as shown in light purple.
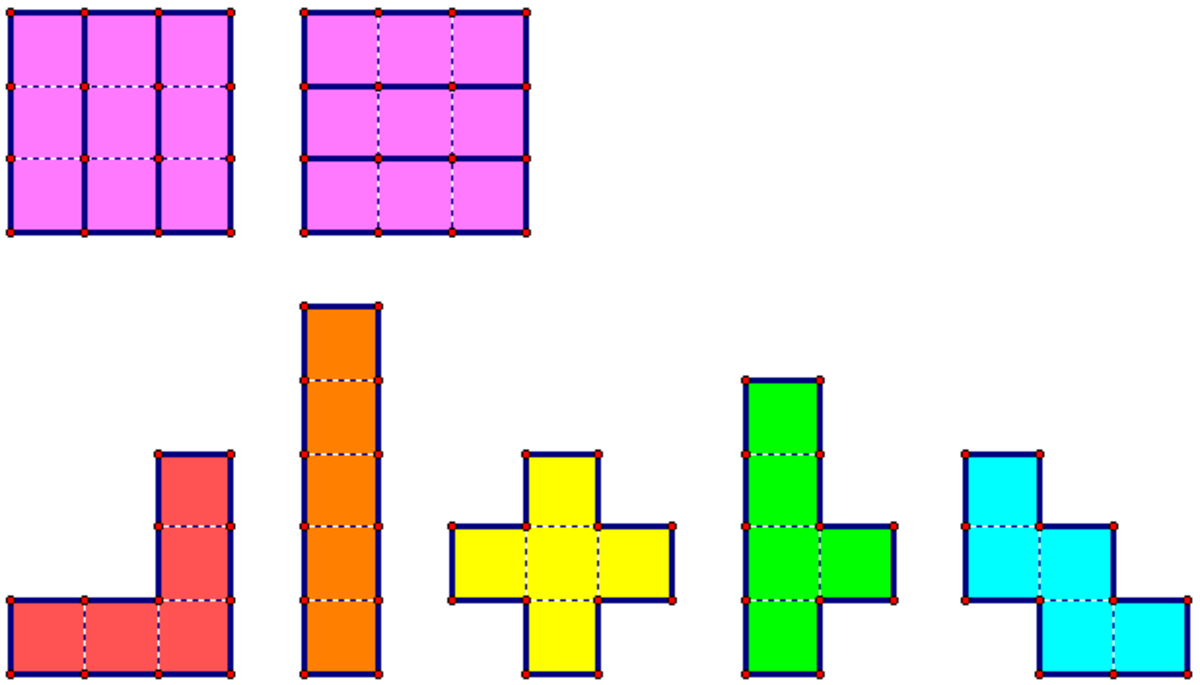
For each of the pentominos, determine the Galvagni figure number and concatenate these numbers in order to create a 5-digit number. (Hint: one of the shapes has no Galvagni figure. Put for it).
The answer is 24024.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The picture shows the Galvagni figure for each and why the numbers for each are 2, 4, 0, 2, 4. The last one is interesting because there are 3 ways to tile it.
Incidentally, the concept is actually named after me. I proposed this as an extension to a problem on a monthly problem site quite a few years ago. However, I did not discover most of the actual figures.