Gamble Machine
See the picture below.
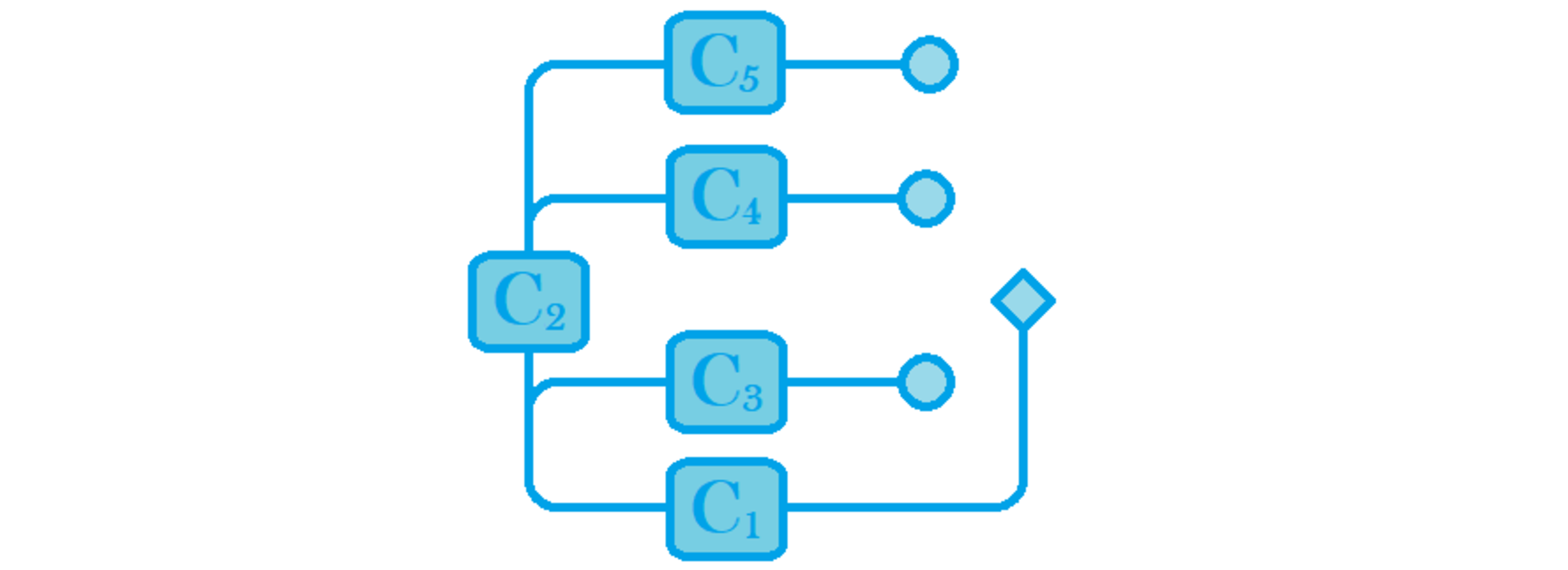
The picture shows a button (the diamond), which leads to five small contraptions (the boxes with in them C 1 , … , C 5 ), which in the end lead to three light bulbs (the circles). When the button is pressed, a signal is passed. The signal will first be passed to C 1 , as can be seen in the picture. Each contraption has 5 0 % chance to pass along the signal to the next contraption(s) or light bulb, otherwise the signal will not be passed along to the next contraption(s) or light bulb. When the signal is passed along to a light bulb, the light bulb will turn on. This whole process continues until all the light bulbs are turned on or until the light bulbs which are not turned on can't be reached by the signal anymore (due to the fact that the signal is not passed along a contraption before that lightbulb).
This machine can be used as a gamble machine as will be explained now. A player can put in n ∈ Z > 0 amount of coins, after which he can press the button. If 0 light bulbs turn on, the player gets nothing back. Else, if i ∈ { 1 , 2 , 3 } light bulbs turn on, the player will get ( i + 1 ) n coins back.
If the player puts in one coin, the expected loss of the player can be written as b a , where a and b are coprime positive integers. Calculate a + b .
The answer is 37.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I did it the same way, but I wonder if there is a more efficient way of solving this. This is an amazing problem, did you make it up?
Log in to reply
A friend of mine made this gamble machine in a specific game to make money and because I kept winning the game as a player I was curious how he made it and wanted to calculate if this machine was in fact in favor of the casino in the long run.
For each
i
, let the indicator variable
C
i
denote the event that the
i
th bulb is ON and
C
i
c
≡
1
−
C
i
. Hence, the number of light bulbs
N
which are on may be expressed as
N
=
C
1
C
3
+
C
1
C
2
C
4
+
C
1
C
2
C
5
.
Using linearity of expectation and independence, the expected number of bulbs which are ON may be computed as:
E
(
N
)
=
2
1
⋅
2
1
+
2
1
⋅
2
1
⋅
2
1
+
2
1
⋅
2
1
⋅
2
1
=
2
1
.
Next we will compute the probability of the event
F
that all bulbs are off. From the circuit diagram, this event can be expressed as
F
=
C
1
c
+
C
1
C
3
c
(
C
2
c
+
C
2
C
4
c
C
5
c
)
.
Taking expectation of both sides and using linearity of expectation and independence, we have
P
(
F
)
=
2
1
+
2
1
⋅
2
1
(
2
1
+
2
1
⋅
2
1
⋅
2
1
)
=
3
2
2
1
.
Note that the player loses one coin when the event
F
takes place. Thus, the expected loss of the player is given by
3
2
2
1
−
2
1
=
3
2
5
.
I solved this problem by creating a scheme of the possible outcomes, see the scheme at the end of this solution. For now, we ignore the last two columns. A "0" in a column i ∈ { 1 , … , 5 } means that in that possible situation C i does not pass along the signal. Else, it is "1" and it does pass along the signal. As an example, the row ( 1 , 0 , 1 , 1 , 0 ) is not possible because C 2 did not pass along the signal to C 4 , which means that C 4 could not pass along the signal to the light bulb following it.
Now we have to calculate for each of those possible scenarios the chance it will happen. In the scheme, I have put this under the label P . To safe the most calculations, I will go over two of these possibilities, namely ( 0 , 0 , 0 , 0 , 0 ) and ( 1 , 1 , 1 , 0 , 1 ) . The other cases will be similar. For the first case, notice that C 1 leads towards all the other contraptions, which makes the other four contraptions not working as well. Because the chance that C 1 = 0 is equal to 5 0 % , we see that the chance on the first scenario happening is equal to 2 1 = 3 2 1 6 . For the latter case, we see that C 1 , C 2 , C 3 and C 5 are on. Because C 1 leads into C 2 and C 3 , and furthermore C 2 leads into C 4 and C 5 , we notice that every contraption is reached by the signal, which makes chance on this scenario happening equal to ( 2 1 ) 5 = 3 2 1 .
Lastly, we have to calculate how many light bulbs are turned on in every case, in the scheme this is put under the label # L . This is easy, because it is not hard to observe that the number of light bulbs turned on is equal to the sum of the terms in the corresponding row; columns 3, 4 and 5.
Calculating the expected gain of the player is now simply calculating the product of the last column and the number of coins corresponding to the number of light bulbs turned on. We then add them together minus the coin he put in. We get 0 ⋅ 3 2 1 6 + 4 + 1 + ( 1 + 1 ) ⋅ 3 2 4 + 1 + 1 + 1 + ( 2 + 1 ) ⋅ 3 2 1 + 1 + 1 + ( 3 + 1 ) ⋅ 3 2 1 − 1 = − 3 2 5 , so the expected loss is 3 2 5 , resulting in the answer 5 + 3 2 = 3 7 .
Here the scheme I was talking about: