Garden Border Problem

Number Theory Level 2

A landscaper has been commissioned to plant a rectangular garden of red roses surrounded by a border garden of yellow roses that is 3 feet on each side, as shown below, but in such a way that the area of the red roses is equal to the area of the yellow roses.

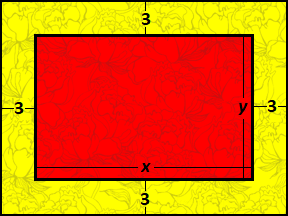
He finds one set of integer solutions for the red rose garden to be 30 feet by 9 feet (and by symmetry 9 feet by 30 feet), since both the red rose garden and the yellow rose garden would both have an equal area of 270 square feet. Are there any other integer solutions possible?

yes, infinitely many no yes, finitely many

1 solution

David Vreken
Apr 11, 2018

The red rose garden has an area of $xy$ , and the yellow rose garden has an area of $(x + 6)(y + 6) - xy$ . When both areas are equal, $xy = (x + 6)(y + 6) - xy$ which simplifies to $y = \frac{6(x + 6)}{x - 6}$ and further to $y = 6 + \frac{72}{x - 6}$ .

Therefore, integer solutions coincide with all the integer divisors of $72$ (which solves to $(7, 78)$ , $(8, 42)$ , $(9, 30)$ , $(10, 24)$ , $(12, 18)$ , and $(14, 15)$ ) which is a finite set.

Garden Border Problem

1 solution

0 pending reports