Garden Path

Geometry Level 4

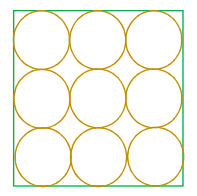Nine unit circles are packed into a square, tangent to their neighbors and to the square. Consider the paths that connect two opposite corners of the square subject to the following conditions:

The path is continuous
The path is (once) differentiable, meaning that it doesn't change direction suddenly.
The path may not touch or cross itself.

What is the length of the longest path?

The answer is 28.704.

1 solution

Marta Reece
May 13, 2017

The longest possible paths are pictured on the left.

For each of them there are three additional paths which can be obtained by rotation and/or reflection. But all eight of them are the same length.

The paths all consists of two straight segments, each $1$ long, and a curved section the length of which we can calculate by first counting the number of quarter circles each circle contributes in turn, which is:

$2+3+1+1+3+1+1+3+2=17$

Or in the second case:

$2+2+1+3+2+1+3+2+1=17$

The length of the path is:

$2 + \frac 14 \times 17\times 2\pi=2+\dfrac{17\pi}{2}\approx\boxed{28.704}$

You haven't proven that those paths are indeed maximum.

Ivan Koswara - 4 years ago

Nice problem.

Hana Wehbi - 4 years ago

Garden Path

The answer is 28.704.

1 solution

0 pending reports