Gather your friends and Practice it

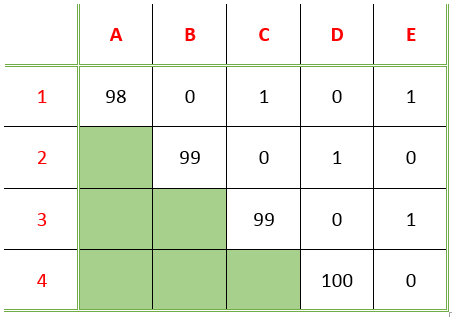
Assumptions :

$\boxed{\text{The captain is the pirate 5, the senior most of all} \\ \text{the second senior most being pirate 4,} \\ \text{ the third senior most being pirate 3,} \\ \text{the fourth senior most being pirate 2} \\ \text{and the most junior being pirate 1.}}$

The captain says he will take $98$ coins, and will give one coin to the third most senior pirate and another coin to the most junior pirate. He then explains his decision in a manner like this :

CASE 1: If there were only 2 pirates left. Pirate 2 being the most senior, he would just vote for himself and that would be $50\%$ of the vote,and pirate 1 would get nothing. and pirate 2 is obviously going to keep all the money for himself.

CASE 2: If there were only 3 pirates left . Pirate 3 has to convince at least one other person to join in his plan. Pirate 3 would take $99$ gold coins and give 1 coin to pirate 1. Pirate 1 knows if he does not vote for pirate 3, then he gets nothing (since if he doesn't join the plan, Pirate 3 is killed & CASE 1 comes in action where he doesn't get anything.) So obviously pirate 1 is going to vote for this plan.

CASE 3: If there were 4 pirates left . Pirate 4 would give $1$ coin to pirate 2, and pirate 2 knows if he does not vote for pirate 4, then he gets nothing (since if he doesn't join the plan Pirate 4 is killed & CASE 2 comes in action where he doesn't get anything). So obviously he is going to vote for this plan.

Finally now there are 5 pirates , so the captain would give one coin each to pirate 1 and pirate 3 since they know that if they don't vote for pirate 5,then they will get nothing (as Pirate 5 will be killed and CASE 3 will come in action). So obviously they are going to vote for this plan.

So, the captain can get maximum of $\boxed{98 coins}$ .

Let's start by naming them from the captain down to the cabin boy ;)

A, B, C, D, & E

Now we have 4 Iterations\cases, the logical approach to solve such problem is to start from the last case back to the first state

Remember the proposal passes by 50% or more so 50% is enough for it and also that every one thinks of what is best for himself only, they don't scheme together nor play it fair (hint their greed drives them)

You will notice that the last state\case is the key to all this

Of course there is a hint missing or let's say it's included but should be emphasized which is "if any pirate finds out that he'll get the same amount of coins whether he agreed or not to the proposal he'll say no"

See this TED video

and if there were $n$ pirates?is there are formula for this?