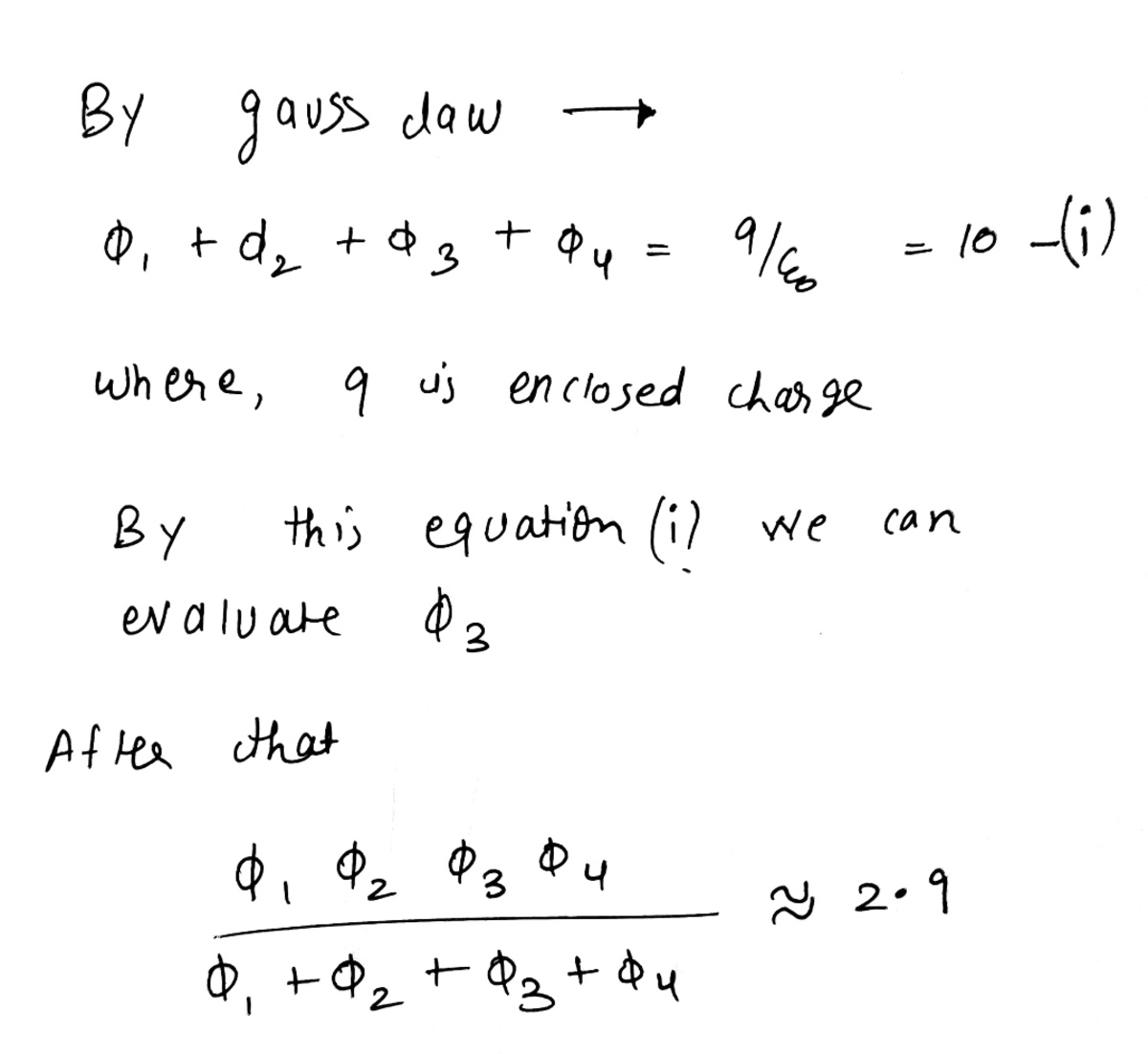Gauss's Law - Closed Half Cylinder
A particle with charge q = + 1 0 is at position ( x , y , z ) = ( 2 1 , 3 1 , 3 2 ) . A closed surface consists of four sub-surfaces put together.
The first sub-surface is a half-disk in the plane z = 0 :
x 2 + y 2 ≤ 1 x ≥ 0 z = 0
The second sub-surface is a half-disk in the plane z = 1 :
x 2 + y 2 ≤ 1 x ≥ 0 z = 1
The third sub-surface is a half cylinder:
x 2 + y 2 = 1 x ≥ 0 0 ≤ z ≤ 1
The fourth sub-surface is a rectangle:
x = 0 − 1 ≤ y ≤ 1 0 ≤ z ≤ 1
Let the electric fluxes through the four sub-surfaces be ϕ 1 , ϕ 2 , ϕ 3 , ϕ 4 . Determine the following ratio:
ϕ 1 + ϕ 2 + ϕ 3 + ϕ 4 ϕ 1 ϕ 2 ϕ 3 ϕ 4
Details and Assumptions:
1)
Electric permittivity
ϵ
0
=
1
2)
Use outward-facing normal vectors
The answer is 2.9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I will not elaborate all the things that how I reached these integral expression, if you see old questions of this type only then @Karan Chatrath Sir has explained it in a very explanatory manner that how to reach this integral expressions. For calculating ϕ 1 and ϕ 2 I have used polar coordinates and for ϕ 4 I have used simple cartesian coordinates.