Gauss's Law Exercise (Part 2)

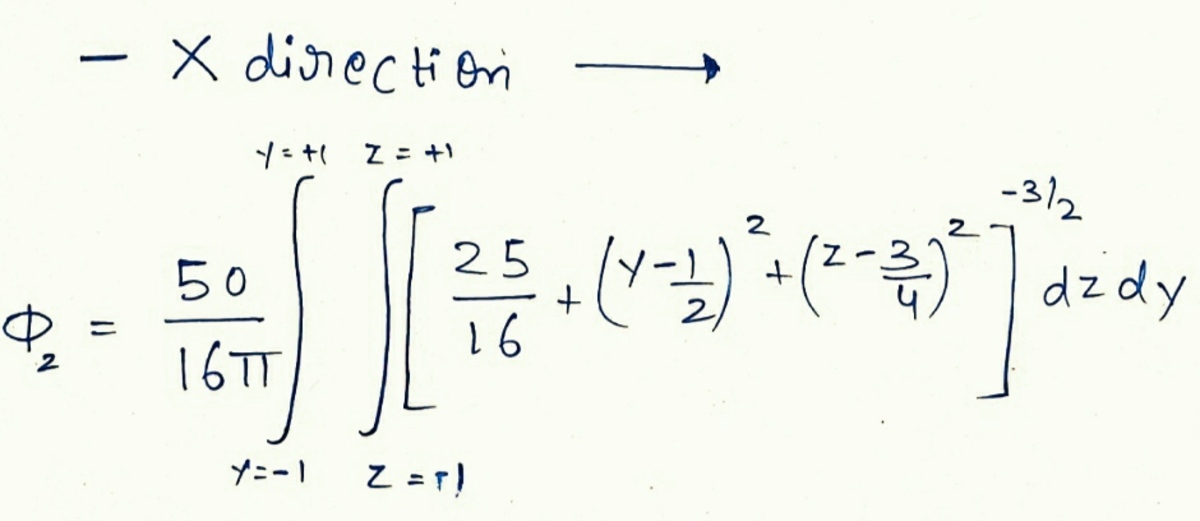
I will show the working for computing the electric flux through the plane of the cube, passing through the point $(1,0,0)$ and which is perpendicular to the X-axis. Consider a point $P$ on this plane. Its position vetor is:

$\vec{r}_p = 1 \hat{i} + y \hat{j} + z \hat{k}$

The location of the charge has a position vector:

$\vec{r}_c = 0.25 \hat{i} + 0.5 \hat{j} + 0.75 \hat{k}$

The vector joining these two points and directed away from the charge is:

$\vec{r} = \vec{r}_p - \vec{r}_c$

The electric field at point $P$ due to the point charge $+q$ is:

$\vec{E} = \frac{q}{4 \pi \epsilon_o}\left(\frac{\vec{r}}{\lvert \vec{r} \rvert^3}\right)$

Recall that area vectors are outward normals. The surface area element on the plane is:

$d\vec{S} = dy \ dz \hat{i}$

The flux through thhis elementary area due to this electric field is:

$d\phi_1 = \vec{E} \cdot d\vec{S}$

Substituting and simplifying gives:

$d\phi_1 = \frac{10}{4 \pi} \left(\frac{\left(1 - 0.25\right)dz \ dy}{\left( \left(1 - 0.25\right)^2 + \left(y - 0.5\right)^2 + \left(z - 0.75\right)^2\right)^{3/2}}\right)$

Finally,

$\phi_1 = \int_{-1}^{1} \int_{-1}^{1} \frac{10}{4 \pi} \left(\frac{\left(1 - 0.25\right)dz \ dy}{\left( \left(1 - 0.25\right)^2 + \left(y - 0.5\right)^2 + \left(z - 0.75\right)^2\right)^{3/2}}\right) \approx 1.56226$

The above integral is computed using Wolfram-Alpha. Similarly, for other planes that make up the cube:

The plane of the cube, passing through the point $(-1,0,0)$ and which is perpendicular to the X-axis: $\phi_2 = \int_{-1}^{1} \int_{-1}^{1} \frac{10}{4 \pi} \left(\frac{\left(1 + 0.25\right)dz \ dy}{\left( \left(1 + 0.25\right)^2 + \left(y - 0.5\right)^2 + \left(z - 0.75\right)^2\right)^{3/2}}\right) \approx 0.960058$

The plane of the cube, passing through the point $(0,0,1)$ and which is perpendicular to the Z-axis: $\phi_3 = \int_{-1}^{1} \int_{-1}^{1} \frac{10}{4 \pi} \left(\frac{\left(1 - 0.75\right)dx \ dy}{\left( \left(x - 0.25\right)^2 + \left(y - 0.5\right)^2 + \left(1 - 0.75\right)^2\right)^{3/2}}\right) \approx 3.66651$

The plane of the cube, passing through the point $(0,0,-1)$ and which is perpendicular to the Z-axis: $\phi_4 = \int_{-1}^{1} \int_{-1}^{1} \frac{10}{4 \pi} \left(\frac{\left(1 + 0.75\right)dx \ dy}{\left( \left(x - 0.25\right)^2 + \left(y - 0.5\right)^2 + \left(1 + 0.75\right)^2\right)^{3/2}}\right) \approx 0.728906$

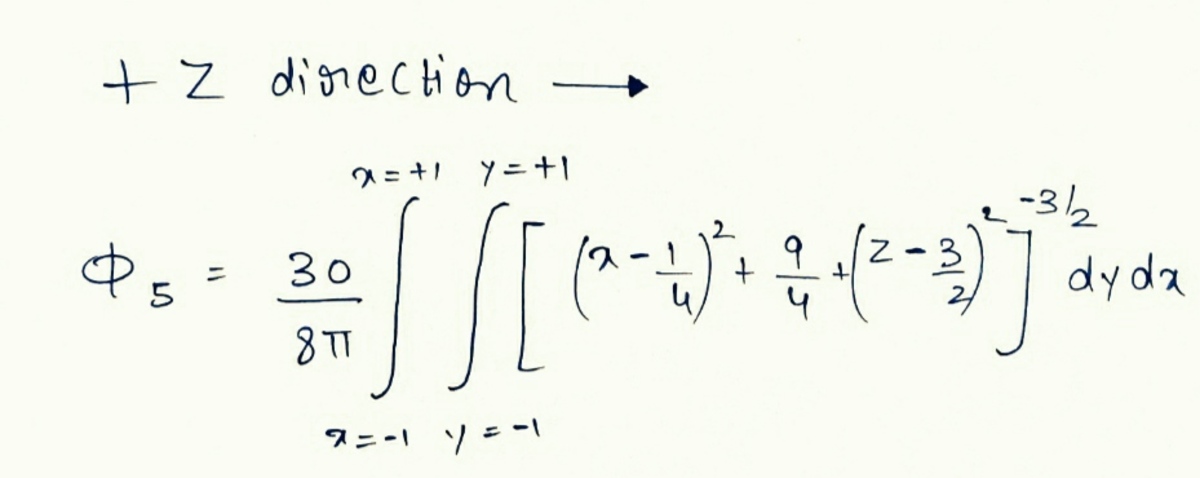
The plane of the cube, passing through the point $(0,1,0)$ and which is perpendicular to the Y-axis: $\phi_5 = \int_{-1}^{1} \int_{-1}^{1} \frac{10}{4 \pi} \left(\frac{\left(1 - 0.5\right)dz \ dy}{\left( \left(x - 0.25\right)^2 + \left(1 - 0.5\right)^2 + \left(z- 0.75\right)^2\right)^{3/2}}\right) \approx 2.26019$

The plane of the cube, passing through the point $(0,-1,0)$ and which is perpendicular to the Y-axis: $\phi_6 = \int_{-1}^{1} \int_{-1}^{1} \frac{10}{4 \pi} \left(\frac{\left(1 + 0.5\right)dz \ dy}{\left( \left(x - 0.25\right)^2 + \left(1 + 0.5\right)^2 + \left(z- 0.75\right)^2\right)^{3/2}}\right) \approx 0.822073$

I have not shown the derivation of all integrands because the process is similar to what is shown.

Therefore:

$\boxed{\phi_1 + \phi_2 + \phi_3 + \phi_4 + \phi_5 + \phi_6 \approx 10}$ $\boxed{\phi_1 \phi_2 \phi_3 \phi_4 \phi_5 \phi_6 \approx 7.4478}$

Nice Problem as always.I will upload the solution of the integrals if asked