Gauss's Law Exercise (part 4)

Electricity and Magnetism Level pending

A particle with charge $q=+10$ is position at $(x,y,z)=(1/4,1/4,1/2)$ behind that black dot as shown in figure. A closed Hemisphere centered at the origin has the equation $x^{2}+y^{2}+z^{2}=1$ $(z≥0)$ . Let the electric flux through through curved surface be $\phi_1$ and through plane surface $\phi_2$

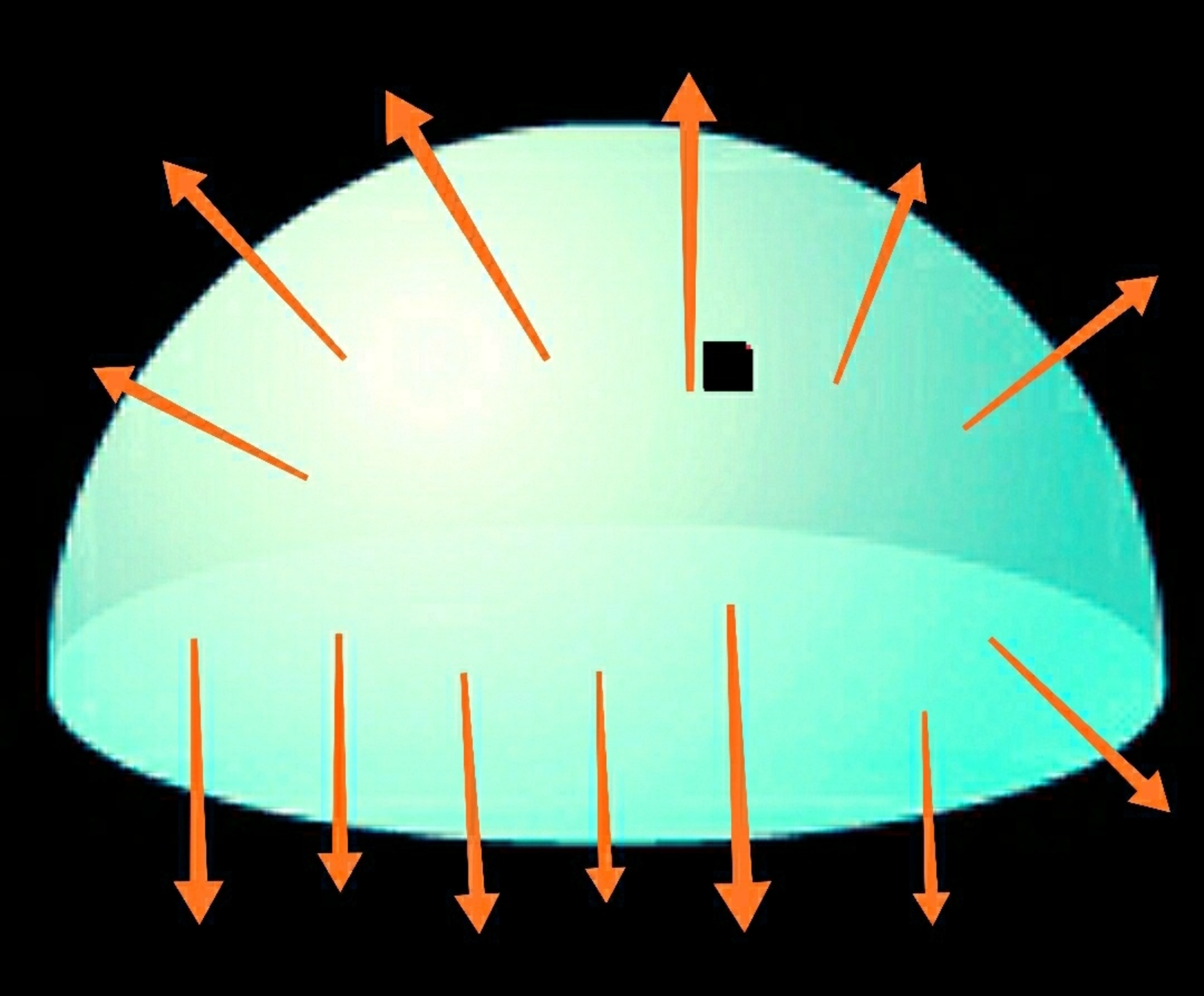
Determine the following ratio: $\frac{\phi_{1}\phi_{2}}{\phi_{1}+\phi_{2}}$ Details and Assumtions 1) Electric permittivity $\epsilon_0=1$ . 2) Area vectors are outward normals .

The answer is 1.934.

1 solution

Steven Chase
Mar 14, 2020

Nice problem. I have attached my simulation code. The fluxes are (where Surface $1$ is the disk):

$\phi_1 \approx 2.623 \\ \phi_2 \approx 7.376$

The fluxes add to $10$ as they must.

import math

N = 5000

#####################################

q = 10.0

xq = 1.0/4.0
yq = 1.0/4.0
zq = 1.0/2.0

e0 = 1.0

#####################################

k = 1.0/(4.0*math.pi*e0)

phi1 = 0.0
phi2 = 0.0

#####################################
#####################################
#####################################
#####################################

# Disk 

dr = 1.0/N
dtheta = 2.0*math.pi/N

nx = 0.0
ny = 0.0
nz = -1.0

r = 0.0

while r <= 1.0:

    theta = 0.0

    while theta <= 2.0*math.pi:

        x = r*math.cos(theta)
        y = r*math.sin(theta)
        z = 0.0

        dS = r*dr*dtheta

        Dx = x - xq
        Dy = y - yq
        Dz = z - zq

        D = math.sqrt(Dx**2.0 + Dy**2.0 + Dz**2.0)

        ux = Dx/D
        uy = Dy/D
        uz = Dz/D

        E = k*q/(D**2.0)

        Ex = E * ux
        Ey = E * uy
        Ez = E * uz

        dot = Ex*nx + Ey*ny + Ez*nz

        dphi = dot * dS

        phi1 = phi1 + dphi

        theta = theta + dtheta

    r = r + dr

print "done"

#####################################
#####################################
#####################################
#####################################


# Half sphere

dsigma = (math.pi/2.0)/N
dtheta = 2.0*math.pi/N

sigma = 0.0

while sigma <= math.pi/2.0:

    theta = 0.0

    while theta <= 2.0*math.pi:

        x = 1.0*math.cos(theta)*math.sin(sigma)
        y = 1.0*math.sin(theta)*math.sin(sigma)
        z = 1.0*math.cos(sigma)

        nx = x
        ny = y
        nz = z

        dS = (1.0**2.0)*math.sin(sigma) * dtheta * dsigma

        Dx = x - xq
        Dy = y - yq
        Dz = z - zq

        D = math.sqrt(Dx**2.0 + Dy**2.0 + Dz**2.0)

        ux = Dx/D
        uy = Dy/D
        uz = Dz/D

        E = k*q/(D**2.0)

        Ex = E * ux
        Ey = E * uy
        Ez = E * uz

        dot = Ex*nx + Ey*ny + Ez*nz

        dphi = dot * dS

        phi2 = phi2 + dphi

        theta = theta + dtheta

    sigma = sigma + dsigma

print "done"
print ""
print ""

#####################################
#####################################
#####################################
#####################################

print N
print ""
num =  phi1 * phi2 
denom =  phi1 + phi2 

print phi1
print phi2
print ""

print num
print denom
print ""

print (num/denom)

################################################

#done
#done


#1000

#2.62580284854
#7.38980208395

#19.4041633622
#10.0156049325

#1.93739304745
#>>> ================================ RESTART ================================
#>>> 
#done
#done


#2000

#2.62544373033
#7.38339536989

#19.3846890824
#10.0088391002

#1.93675698933
#>>> ================================ RESTART ================================
#>>> 
#done
#done


#5000

#2.62321801288
#7.37643115336

#19.3499870723
#9.99964916624

#1.9350665959

Gauss's Law Exercise (part 4)

The answer is 1.934.

1 solution

0 pending reports