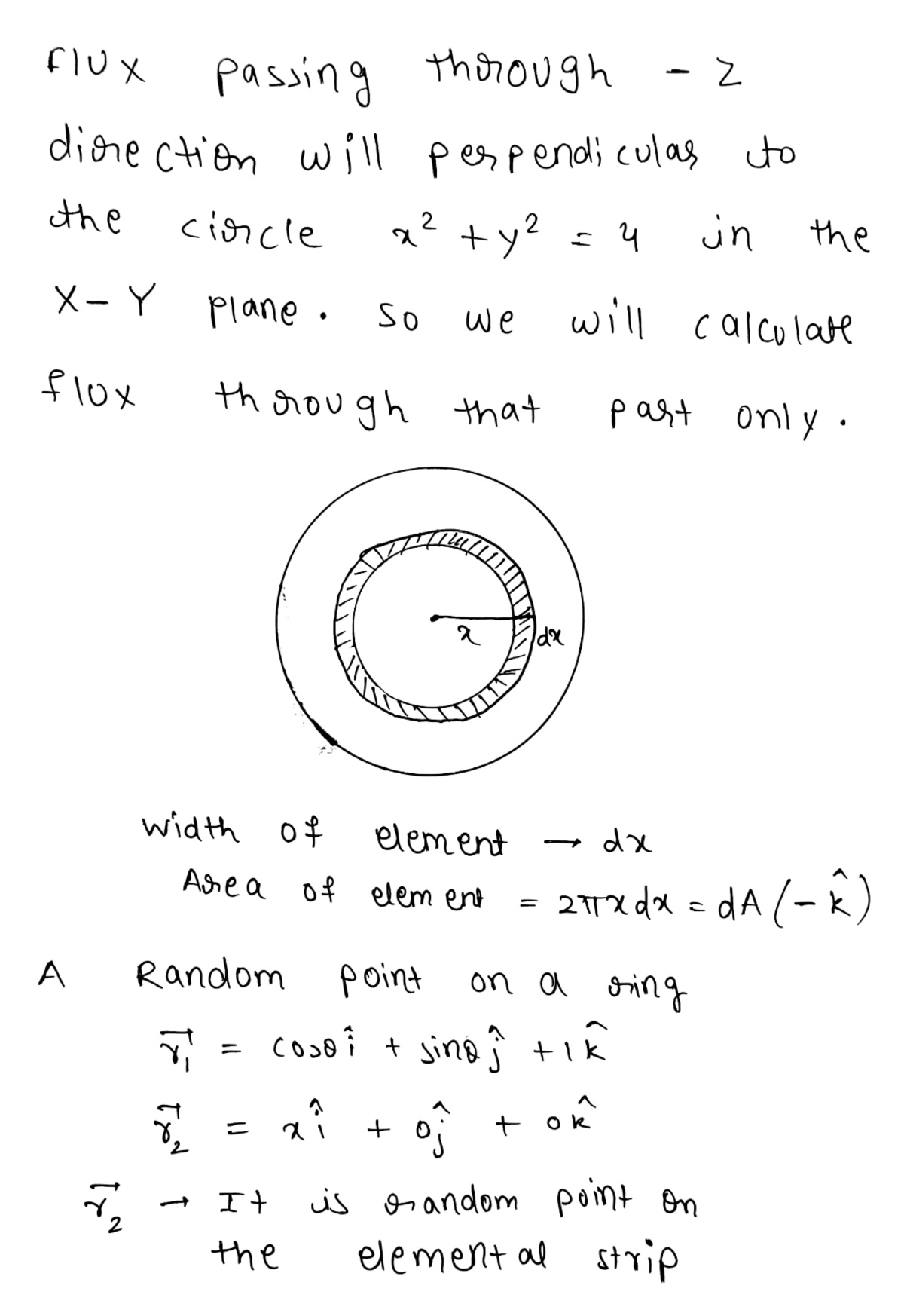
Gauss's Law - Ring of Charge
A ring of charge is defined as follows:
The ring has units of charge per unit length. Let be the electric flux through the half of a sphere of radius centered on the origin, and let be the electric flux through the half.
Determine the following ratio:
Details and Assumptions:
1)
Electric permittivity
2)
Use outward-facing surface normal vectors
Note: I probably should have rated this "Hard", but I clicked "Medium" instead
The answer is 1.17.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Nice Problem.