Gemetry Revisited 3
If a rectangle is inscribed in a semicircle of radius 5 .Find the maximum possible area of that rectangle.
Interesting? Try more problem of this set - Geometry Revisited .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I used AM-GM Inequality.
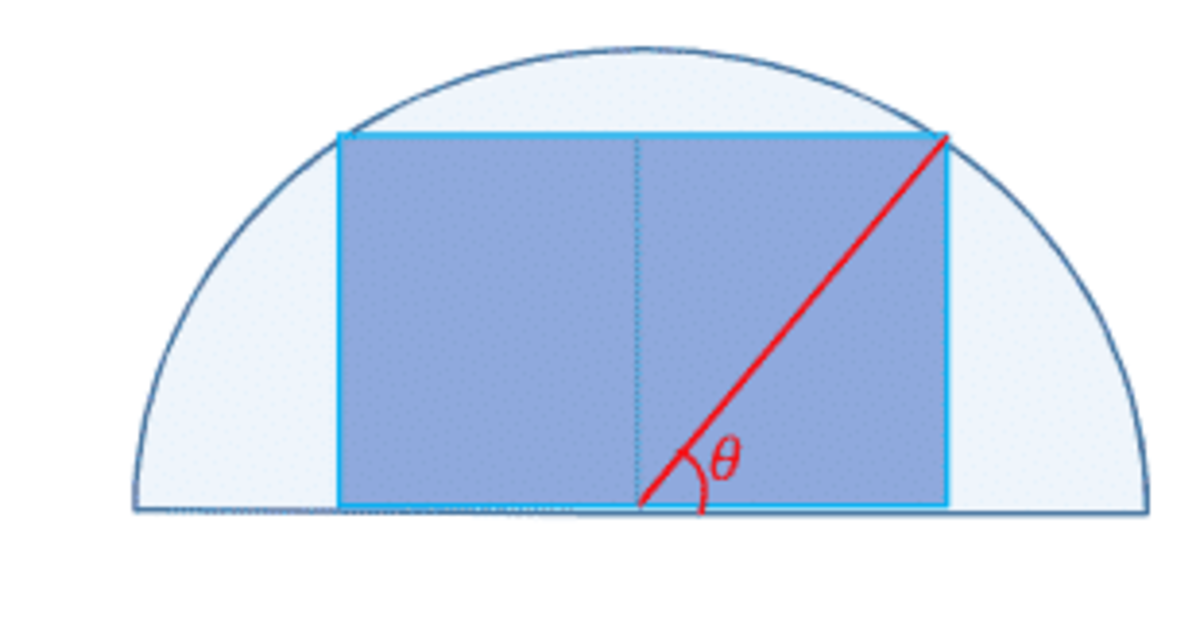 For simplicity, let's do most of the calculation with radius equal
1
, then scale up.
The height of the rectangle is
s
i
n
(
θ
)
, half the width is
c
o
s
(
θ
)
, so the area of the rectangle is
A
=
2
s
i
n
(
θ
)
c
o
s
(
θ
)
=
s
i
n
(
2
θ
)
.
For simplicity, let's do most of the calculation with radius equal
1
, then scale up.
The height of the rectangle is
s
i
n
(
θ
)
, half the width is
c
o
s
(
θ
)
, so the area of the rectangle is
A
=
2
s
i
n
(
θ
)
c
o
s
(
θ
)
=
s
i
n
(
2
θ
)
.
The function s i n ( 2 θ ) has a maximum at θ = 4 5 ∘ so the height of the rectangle will be 2 1 and the width twice that or 2 giving us area of 2 1 × 2 = 1 .
Scaling will multiply all distances by 5 , so the area will be 5 times more, or 5.
I did it with trigonometry but I used the law of the triangle area = absin@/2
Let xy be the coordinates of the top right vertex of the rectangle, and origin as the center of the semicircle.
A r e a f ( A ) = 2 ∗ x ∗ y , ∴ f ( A m a x ) = 2 y + 2 x d x d y = 0 . B u t x 2 + y 2 = 5 , ⟹ 2 x + 2 y d x d y = 0 , ⟹ d x d y = − y x . ∴ 2 y + 2 x ∗ ( − y x ) = 0 , ⟹ x 2 = y 2 . Substituting in the equation of the semicircle, since y>0, we get y = 2 5 , x = ± 2 5 . f ( A m a x ) = 2 ∗ x ∗ y = 5