Gems of Geometry
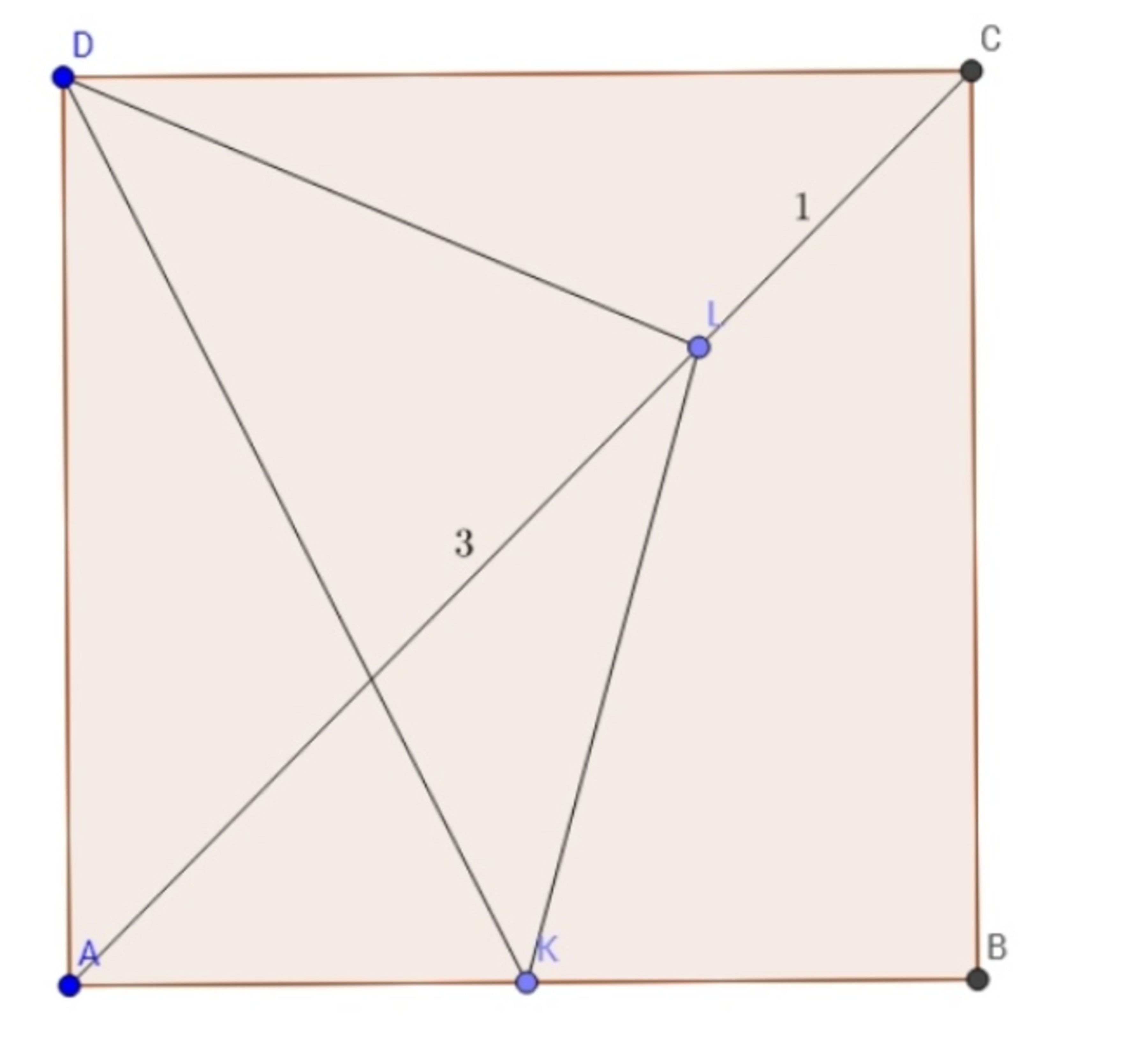
In the figure, A B C D is a square. K is the midpoint of A B . L is a point on A C such that
L C A L = 1 3 . Find the measure of ∠ K D L in degrees.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice approach. When wanting to determine a triangle, it helps to obtain their side lengths (or angles) where possible.
I used stewarts theorem and cosine rule.
∠ D L K = 9 0 o so D L K A cyclic and ∠ L D K = ∠ L A K = 4 5 o
We see that triangle DLA and MLC are similar. .'. CM = x/3. Now we copy the triangle DCM as DAM' . Then we find DM' and DK. Finally draw a perpependicular on DK to find angle M'DK. or just using cosine rule we can find that. .'. Our requIred angle is 45 degrees.
An easier way would be to prove that LK=LB and also that angle DLK =90°.
That would require the same amount of work.
Once you find out that particular angle by anyway there are numerous geometric ways coming in your mind.
Can you elaborate on the sequence of steps that you took? It is not clear to me what you're doing here.
Log in to reply
The given way is one of the easiest while there may be many ways to approach to the solution.
We see that triangle DLA and MLC are similar. .'. CM = x/3. Now we copy the triangle DCM as DAM' . Then we find DM' and DK. Finally draw a perpependicular on DK to find angle M'DK. or just using cosine rule we can find that. .'. Our requIred angle is 45 degrees.
Log in to reply
Can you add that information in the solution itself? Thanks.
Much better. Thanks!
In the figure above,
Let A L = 3 x and L C = x .
Then by Pythagoras theorem in △ A B C
⇒ ( 4 x ) 2 = ( A B ) 2 + ( B C ) 2 ⇒ ( A B ) 2 = 8 x 2 ⇒ A B = 2 2 x .
So, that A K = K B = x 2 . Also A D = 2 2 x as A B C D is a square.
As A C is a diagonal, ∠ D A C = 4 5 0 .
By cosine rule in △ A L D ,
⇒ cos 4 5 = 2 ( A D ) ( A L ) ( A D ) 2 + ( A L ) 2 − ( D L ) 2 ⇒ 2 1 = 1 2 2 x 8 x 2 + 9 x 2 − ( D L ) 2 ⇒ D L = x 5 .
Again applying Cosine rule in △ A K L with ∠ K A L = 4 5 0 , We get
L K = x 5 .
Now by pythagoras theorem in △ A D K , we have
D K = x 1 0 .
Observe in △ L D K
D K 2 = 1 0 x 2 = 5 x 2 + 5 x 2 = ( L D ) 2 + ( L K ) 2 .
Which implies ∠ D L K = 9 0 0 .
Also, as L K = L D
⇒ ∠ K D L = 4 5 0 .