General knowledge test about magnetic fields
Electricity and Magnetism
Level
3
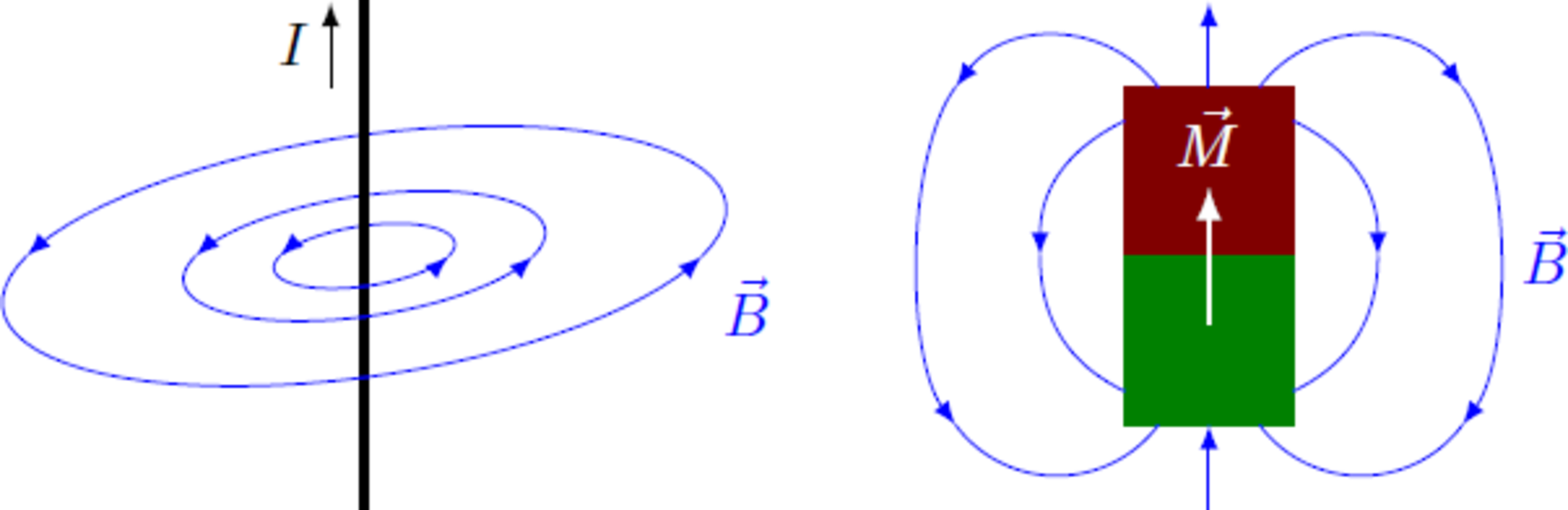
Which of the following statements about magnetic fields are true?
- (A) The field lines of the magnetic flux density describe possible paths of electric charges under the influence of the Lorentz force.
- (B) The field lines of magnetic flux density are always closed curves.
- (C) A homogeneous magnetic field exerts a net force on a static magnet.
- (D) The vectors and are always aligned parallel to each other.
Only (D) is true.
All statements are true.
Only (C) and (D) are true.
Only (C) is true.
Only (B) is true.
Only (A) is false.
Only (A) and (B) are true.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The field lines of the magnetic flux density describe possible paths of electric charges under the influence of the Lorentz force. :
The Lorentz force F L = q v × B , which acts on a charge q with velocity v , is always perpendicular to the magnetic field B . Therefore, the charge is deflected perpendicularly to B and forced on circular paths around the magnetic field line. If the charge should (coincidentally) follow the course of the magnetic field line, because of v ∥ B the Lorentz force is zero, so that the orbit of the particle is not affected by the magnetic field. The Statement (A) is therefore false.
The field lines of magnetic flux density are always closed curves.
Gauss' law for magnetism is ∇ ⋅ B = 0 and states that the magnetic flux density is free of sources and thus there are no magnetic monopoles. This equation can be transformed by applying the Gaussian theorem to ∮ B ⋅ d A = 0 . That is, the magnetic flux through a closed surface of any volume is zero. If a magnetic field line penetrates a volume, it must also exit at another point and must not end in volume, so that the field lines are always closed. Statement (B) is therefore true. (However, this statement generally does not apply to the magnetic field H .)
A homogeneous magnetic field exerts a net force on a static magnet.
A magnet with magnetization M and volume V in an external magnetic field H has the potential energy W mag = − 2 μ 0 V H c d o t M . The energy depends on the orientation of the vector M and becomes minimal if it is parallel to H . Therefore, a torque acts on the magnet, which aligns it parallel to the external magnetic field. However, no net force is present in a homogeneous field H = const , because the potential energy is independent of the position of the magnet. The statement (C) is therefore wrong.
The vectors B and H are always aligned parallel to each other.
In a vacuum, the magnetic fields are simply linked by the equation B = μ 0 H . For an isotropic diamagnetic or parametric material, the equation alters to B = μ 0 ( 1 + c h i ) H with the susceptibility χ , so that both vectors are identical except for a scalar prefactor. However, the magnetization M of a ferromagnet is not always aligned parallel to the external field, but has a hysteresis behavior and a remanent magnetization M = M 0 for H = 0 . The magnetization can only be realignend in an sufficiently large external field. Therefore, if a ferromagnet is magnetized along the x-direction ( M = M 0 e x ) and a small external field H = H e y is applied perpendicularly, the resulting flux density B = μ 0 ( H + M ) is not parallel to the field H . The statement (D) is therefore wrong.