Generalized Chinese Puzzle
Consider a body that is formed by the intersection of two identical and perpendicular cylinders. The cross-section of the cylinders has at least one axis of symmetry. Also, the boundary of the half of the cross section can be expressed as a function of this axis (the half cross section is the area under the function).
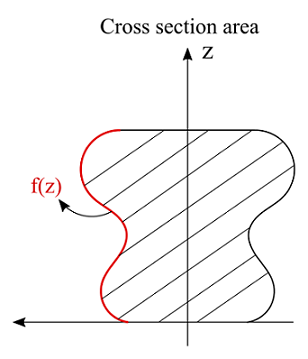 Now consider a second volume created by the revolution of the half cross section area. What is the ratio of the intersection volume to the revolution volume?
Now consider a second volume created by the revolution of the half cross section area. What is the ratio of the intersection volume to the revolution volume?
For example:
Take any function (it can be piecewise).
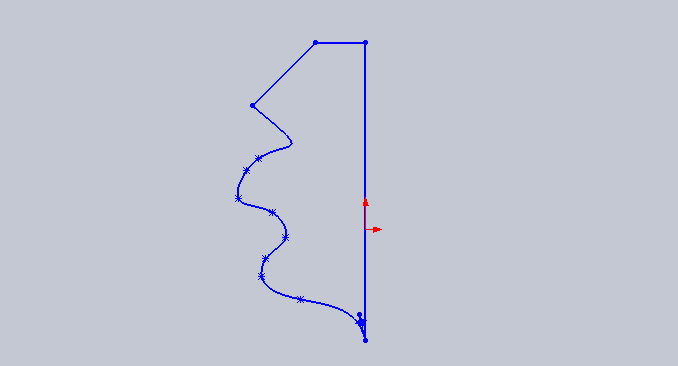 Create the cylinders.
Create the cylinders.
 We get the intersection volume
We get the intersection volume
 We also need the revolution volume
We also need the revolution volume
 And calculate the ratio
.
And calculate the ratio
.
Give your answer to 3 decimal places.
The answer is 1.273239.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We can write the volume of the intersection body as 4 times the volume of the missing part from the solid in the figure. Cosider the height of the body as H . V i n t = 4 V ∫ 1 d V = 4 0 ∫ H 0 ∫ f ( z ) 0 ∫ f ( z ) 1 d x d y d z The final form we will use later is: V i n t = 4 0 ∫ H f ( z ) 2 d z The volume of revolution of the half cross section is equal to the area of half cross section times the length of revolution of the center of the mass. Let's note the distance from the center of mass to z -axis with D . V r e v = A 2 π D Where A is the area under the function. We know the formula for the center of mass: D = A A ∫ k d A = A 0 ∫ H ( 0 ∫ f ( z ) k d k ) d z Where k is the axis perpendicular to z -axis ( the coordinate of element d A ). Substituting and simplifying the area we get: V r e v = 2 π 0 ∫ H ( 2 k 2 ∣ ∣ ∣ ∣ 0 f ( z ) ) d z = π 0 ∫ H f ( z ) 2 d z We see now that the ratio is: V r e v V i n t = π 4 ≈ 1 . 2 7 3 2