Generator Powers

Electricity and Magnetism Level 4

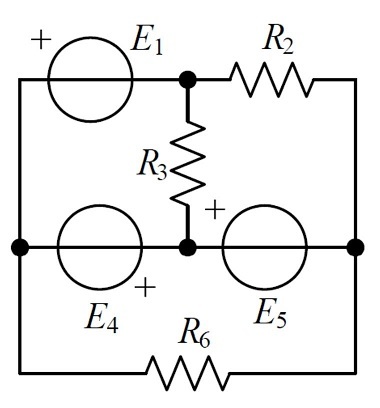
In the circuit above, we have three generators E 1 E_1 , E 4 E_4 , and E 5 E_5 . Calculate their powers P 1 P_1 , P 2 P_2 , and P 3 P_3 , and input your answer as the sum of the three powers in milliwatts.

Details and Assumptions:

  • E 1 = 10 V E_1 = 10 \text{ V} , E 4 = 5 V E_4 = 5 \text{ V} , E 5 = 3 V E_5 = 3 \text{ V} , R 2 = 6 k Ω R_2 = 6 \text{ k}\Omega , R 3 = 5 k Ω R_3 = 5 \text{ k}\Omega , and R 6 = 2 k Ω R_6 = 2 \text{ k}\Omega
  • It is possible that one or more generators have negative powers.
  • The lines across the generators mean that they are ideal with 0 Ω 0 \ \Omega internal resistance.


The answer is 71.

Djordje Veljkovic by Djordje Veljkovic , 19, Serbia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Steven Chase
May 23, 2017

Since the sources are ideal, the node voltages are easily determined by adding and subtracting source voltages. See the image above. We know that the sum of the source powers must equal the sum of the resistor powers. Since the power through a resistor can be expressed as P = V 2 R P = \frac{V^2}{R} , we have the following:

P t o t a l = ( 15 − 0 ) 2 5 k + ( 12 − 0 ) 2 6 k + ( 12 − 10 ) 2 2 k = 71 m W \large{P_{total} = \frac{(15 - 0)^2}{5k} + \frac{(12 - 0)^2}{6k} + \frac{(12 - 10)^2}{2k} = \boxed{71 mW}}

4 Helpful 0 Interesting 0 Brilliant 0 Confused
Djordje Veljkovic
May 22, 2017

To find the powers of these generators, we need to know the currents that flow through their respective branches. I will solve this circuit using the C o n t o u r C u r r e n t s M e t h o d Contour\space Currents\space Method . First, we need to see how many contours we need. It is clear to see that we need 3 of them, but let's use the formula to prove it.

N k = N b − ( N n − 1 ) = > N k = 3 N_k\space = \space N_b\space -\space (N_n\space -\space 1)\space =>\space N_k\space = \space 3

N k − t h e n u m b e r o f n e e d e d c o n t o u r s t o s o l v e t h e c i r c u i t N_k\space - \space the\space number\space of\space needed\space contours\space to\space solve\space the\space circuit

N b − t h e n u m b e r o f b r a n c h e s i n t h e c i r c u i t , i n t h i s c a s e 6 N_b\space -\space the\space number\space of\space branches\space in\space the\space circuit,\space in\space this\space case\space 6

N n − t h e n u m b e r o f n o d e s i n t h e c i r c u i t , i n t h i s c a s e 4 N_n\space -\space the\space number\space of\space nodes\space in\space the\space circuit,\space in\space this\space case\space 4

Now, when we know how many contours we need, we can simply assume their directions, as I've done on the picture below.

Now, by definition:

R 11 × I I K + R 12 × I I I K + R 13 × I I I I K = ∑ E I K R_{11}\times I_{IK} + R_{12}\times I_{IIK} + R_{13}\times I_{IIIK} = \sum E_{IK}

R 21 × I I K + R 22 × I I I K + R 23 × I I I I K = ∑ E I I K R_{21}\times I_{IK} + R_{22}\times I_{IIK} + R_{23}\times I_{IIIK} = \sum E_{IIK}

R 31 × I I K + R 32 × I I I K + R 33 × I I I I K = ∑ E I I I K R_{31}\times I_{IK} + R_{32}\times I_{IIK} + R_{33}\times I_{IIIK} = \sum E_{IIIK}

R 11 = R 2 + R 3 = 11 k Ω R_{11} = R_2 + R_3 = 11 kΩ

R 12 = R 21 = R 3 = 5 k Ω R_{12} = R_{21} = R_3 = 5 kΩ

R 22 = R 3 = 5 k Ω R_{22} = R_3 = 5 kΩ

R 13 = R 31 = 0 k Ω R_{13} = R_{31} = 0 kΩ

R 33 = R 6 = 2 k Ω R_{33} = R_6 = 2 kΩ

R 23 = R 32 = 0 k Ω R_{23} = R_{32} = 0 kΩ

∑ E I K = E 5 = 3 V \sum E_{IK} = E_5 = 3 V

∑ E I I K = E 1 + E 4 = 15 V \sum E_{IIK} = E_1 + E_4 = 15 V

∑ E I I I K = E 4 − E 5 = 2 V \sum E_{IIIK} = E_4 - E_5 = 2 V

Substituting these values gives us a system of equations:

11 × I I K + 5 × I I I K = 3 11\times I_{IK} + 5\times I_{IIK} = 3

5 × I I K + 5 × I I I K = 15 5\times I_{IK} + 5\times I_{IIK} = 15

2 × I I I I K = 2 2\times I_{IIIK} = 2

Solving this system gives us:

I I I I K = 1 m A I_{IIIK} = 1 mA

I I K = − 2 m A I_{IK} = -2 mA

I I I K = 5 m A I_{IIK} = 5 mA

Now, for the solution:

∑ P = E 1 × I I I K + E 4 × ( I I I K + I I I I K ) + E 5 × ( I I K − I I I I K ) = 71 m W \sum P = E_1 \times I_{IIK} + E_4 \times (I_{IIK} + I_{IIIK}) + E_5 \times (I_{IK} - I_{IIIK}) = 71 mW

1 Helpful 0 Interesting 0 Brilliant 0 Confused

For those that are unfamiliar with the concept of Contour Currents, here is and explanation to what each of the variables in the system represents:

R 11 - the sum of all the resistors through which I IK flows.

R 22 - the sum of all the resistors through which I IIK flows.

R 33 - the sum of all the resistors through which I IIIK flows.

R 12 / R 21 - the algebraic sum of the resistors through which both I IK and I IIK flow (if they flow in opposite directions we put "-" in front of the resistance value).

R 13 / R 31 - the algebraic sum of the resistors through which both I IK and I IIIK flow.

R 23 / R 32 - the algebraic sum of the resistors through which both I IIK and I IIIK flow.

Sum E IK - the algebraic sum of the electromotive forces of the generators through which I IK flows.

Sum E IIK - the algebraic sum of the electromotive forces of the generators through which I IIK flows.

Sum E IIIK - the algebraic sum of the electromotive forces of the generators through which I IIIK flows.

Djordje Veljkovic - 4 years ago

It's quite easy to calculate the voltages across all three resistors and then use v^2/r.

Steven Chase - 4 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...