Generator with Load Rejection

A single-phase AC electric generator has a moving rotor with a magnet, which induces a voltage $V_t$ at its stator terminals. A resistor $R$ is connected across the stator terminals.

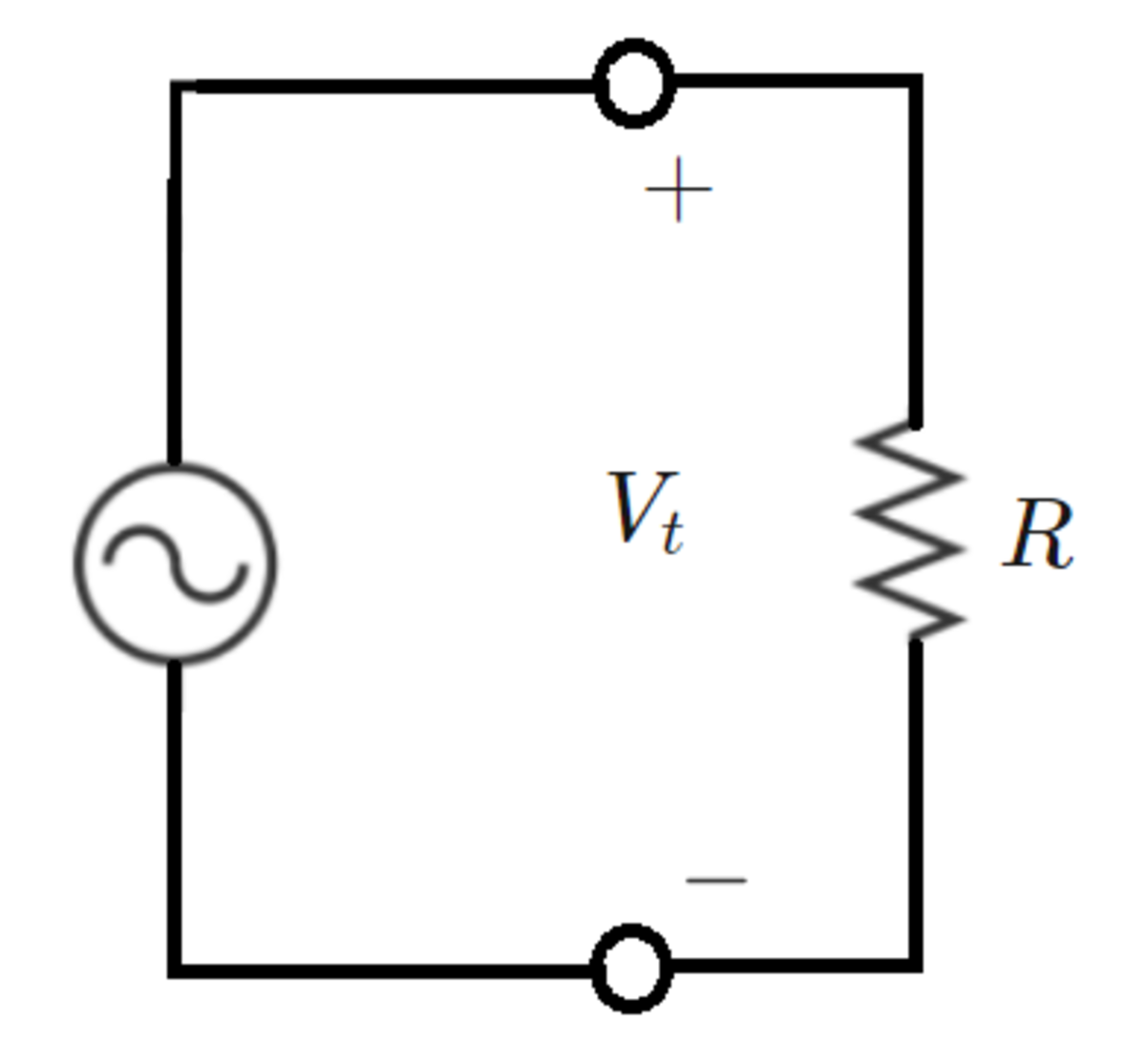
The machine/load model is as follows:

$\lambda = \frac{V_m}{\omega_0} \cos \theta \\ V_t = \dot{\lambda} \\ \frac{d}{dt} \Big(\frac{1}{2} I \dot{\theta}^2 \Big) = P_M-P_R \\ R = R_0 \,\,\,\, \text{for} \,\, 0 \leq t \leq 2 \\ R = 2 R_0 \,\,\,\, \text{for} \,\, t > 2$

In the model, $\lambda$ is the stator magnetic flux linkage as a function of rotor angular position $\theta$ . The terminal voltage $V_t$ is the time derivative of the flux linkage. The third equation states that the rotor is gaining kinetic energy at a rate equal to the difference between the mechanical input power and resistor power dissipation (a statement of energy conservation). The parameter $I$ is the machine inertia constant.

At time $t = 0$ , $\theta = 0$ and $\dot{\theta} = \omega_0$ . The mechanical input power $P_M$ remains fixed. At time $t =2$ , half of the electrical load is disconnected from the generator (modeled as the load resistance doubling). The causes the machine to accelerate until a new steady-state speed is reached.

Determine the following integral:

$\int_2^8 (\dot{\theta} - \omega_0) \, dt$

Bonus: You can predict the final speed very easily without any complicated calculations. How/why is that?

Details and Assumptions (assume standard SI units):
1) $V_m = 120 \sqrt{2}$
2) $\omega_0 = 120 \pi$
3) $R_0 = 15$
4) $I = 0.01$
5) $P_M = \frac{120^2}{R_0}$