Genius Insect!
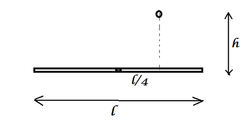 A Thin rod of length
is hinged at the center. An insect falls on it from a height
. The distance of the impact point is
from the center.
A Thin rod of length
is hinged at the center. An insect falls on it from a height
. The distance of the impact point is
from the center.
Apparently, the insect is a
Genius
. To avoid much dizziness, it devices a method to make the rod rotate at
constant
angular velocity. The insect starts
crawling
towards the outer edge of the rod.
Find the height from which the insect drops, such that by the time the rod becomes vertical , the insect reaches the outer edge.
Details and Assumptions:
- The mass of the insect is equal to the mass of the rod
- Neglect air resistance and friction due to the rod.
The answer is 1.701.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let us take an overview of the problem
4 m v l = [ m × ( l / 4 ) 2 + 1 2 m × l 2 ] × ω
T = d t d I w + d t d w I
T = d t d I w
T = 2 m r d t d r ω
Also at any given θ , torque due to insect's weight is m g cos θ × r
m g cos θ × r = 2 m r d t d r ω
Integrating this and substituting limits as
h = 1 . 7 0 1