Gently does it
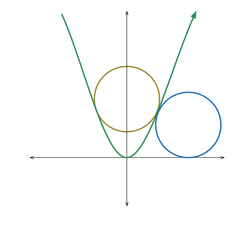 A circle of radius
r
is positioned so that it has two points of tangency with the parabola
y
=
x
2
. Another circle, again of the same radius
r
, is positioned (entirely in the first quadrant) so that it is tangent to both
y
=
x
2
and the positive
x
-axis.
A circle of radius
r
is positioned so that it has two points of tangency with the parabola
y
=
x
2
. Another circle, again of the same radius
r
, is positioned (entirely in the first quadrant) so that it is tangent to both
y
=
x
2
and the positive
x
-axis.
There is a unique value of r so that the two circles described above, both of radius r , are also tangent to one another. If r = b a , where a and b are positive coprime integers, then find a + b .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Nice... I used differentiation. But you didn't. I thought it was impossible to do this without calculus.
Log in to reply
Thanks. Yes, I put this question specifically in the geometry section to see if people could solve it without using calculus. There's nothing wrong with using calculus, of course, but it makes for a more interesting challenge to solve it without. :)
hey can you give calculus approach solution
Many thanks to whomever adds diagrams to my posted questions. Is that you, @Calvin Lin?
can somebody explain how point of tangency is a vertical distance of 0.5 below center of circle 1 thanks
Log in to reply
In the first part of my solution I noted that the y -coordinates of the two points of tangency of the first circle and the parabola are the same, and thus both have the value
( 2 1 ) ( 2 k − 1 ) = k − 2 1 ,
since − 4 k 2 + 1 + 4 r 2 must equal 0 .
Now k is the y -coordinate of the center of the first circle, and so we can conclude that the points of tangency are a vertical distance of 2 1 below the center of the first circle, (and by symmetry also a vertical distance of 2 1 above the center of the second circle).
Brian, this is one of the best problems I've come across on Brilliant, in that choosing the RIGHT way to solve this can make a huge difference how difficult it will be to solve this. I'll post my approach to this problem shortly.
Okay, here it is:
First, let the circles have radius r , the first one centered at ( 0 , r a ) , and the second one centered at ( r b , 0 ) . Because they are tangent, we know that
( r a − r ) 2 + r b 2 = ( 2 r ) 2
From this, we have
b = 3 + 2 a − a 2
The tangent point is at
( 2 r b , 2 r a + r )
And the slope of the tangent line is
r a − r r b
Let the equation of the parabola be (the reason for the coefficients will become clear)
y = k r ( r x ) 2 = ( r k ) x 2
The slope of this parabola is
2 ( r k ) x
Then we solve this system of equations
2 ( r k ) ( 2 r b ) = r a − r r b
( r k ) ( 2 r b ) 2 = 2 r a + r
Ending up with a = 3 5 and k = 2 3 (because r drops out)
Thus, for the parabola to have the form
y
=
x
2
,
r
must be equal to
k
, and we have our answer.
This approach makes careful use of scaling to simplify things.
Thanks, Michael. I look forward to reading your solution.
I like your use of the scaling factors; I'll give that a try on similar problems in the future. Thanks for posting this; our methods are quite different, and hopefully readers will appreciate some aspects of each of them.
Log in to reply
Well, after trying other bashy methods which led nowhere, I decided to try to see what parabola would "thread the needle". Then it became a matter of scaling it to get the right answer.
Let the point of triple intersection be ( t , t 2 ) . The first circle is x 2 + ( y − t 2 − 2 1 ) 2 = r 2 . The second circle is ( x − t ( 2 t 2 − 2 r + 1 ) ) 2 + ( y − r ) 2 = r 2 . Since both pass through ( t , t 2 ) , we get 4 r 2 = 4 t 2 + 1 and ( t − t ( 2 t 2 − 2 r + 1 ) ) 2 + ( t 2 − r ) 2 = r 2 , we solve this system of equations to get r = 2 3 .
 Ujjwal
Ujjwal
(I suggest you sketch the figure and write coordinates of the points)
Let, T(h, h^2) = Common point of tangency for the two circles and parabola
A = y-intercept of tangent. Using property of a parabola : MO = OA
Hence, A = (0, -h^2)
M(0, h^2) = Foot of perpendicular from T on axis
C = Intersection of normal at T and axis
Right triangles AMT & MTC are similar
MT = h, MA = 2 h^2 giving MC = 1/2
Triangles TMC & C2NT are congruent
=> C2 = (2h, h^2-1/2)
=> radius = y coordinate of C2 = h^2 - 1/2 - - - - (I)
But radius is also CT
Pythagoras : CT = sqrt(h^2 + 1/4) - - - - (II)
Solve I & II to get h^2 = 2 and R = 3/2
For the circle tangent in the graph y = x 2 , we want to find how high it is from its points of tangent. Differentiating y = x 2 : d x d y = 2 x Then the gradient of the normal of the graph would be 2 x 1 Since the normal would pass through the center of the circle, using trigonometry, one could derive that the circle would always be 0 . 5 above its points of tangent:
 p
p
Then the relationship between the radius of the circle ( r ) and the height ( y ) is r = 0 . 2 5 + y
For the second circle, we can tell the height would be r + ( s o m e t h i n g ) :
 p
p
where that something is r s i n θ
It can then be derived from the gradient of the normal of the graph the length of that "something". The height with relation to the radius of the second circle can then be expressed: y = r + 4 y + 1 r r = 1 + 4 y + 1 1 y
Since the radius and the height must be the same r = 1 + 4 y + 1 1 y = 0 . 2 5 + y Solving 1 + 4 y + 1 1 y = 0 . 2 5 + y gives y = 2 .
Plugging y = 2 in to the above formula yields r = 2 3 = b a . Therefore, a + b = 5
The center of the first circle will lie on the y -axis. Let the center of this circle be ( 0 , k ) and its radius be r . Then the equation of this circle will be x 2 + ( y − k ) 2 = r 2 . To find the two points of tangency between this circle and the parabola y = x 2 we substitute y = x 2 into the equation of the circle to find that
y + ( y − k ) 2 = r 2 ⟹ y 2 − ( 2 k − 1 ) y + ( k 2 − r 2 ) = 0 .
Employing the quadratic formula, we find that
y = ( 2 1 ) ( ( 2 k − 1 ) ± ( 2 k − 1 ) 2 − 4 ( k 2 − r 2 ) ) ⟹ y = ( 2 1 ) ( ( 2 k − 1 ) ± − 4 k 2 + 1 + 4 r 2 ) .
Now by symmetry the y -coordinates of the two points of tangency must be the same, which implies that the discriminant must equal zero. Thus
− 4 k + 1 + 4 r 2 = 0 ⟹ k = r 2 + 4 1 .
The y -coordinates of the points of tangency are then k − 2 1 = r 2 − 4 1 . Now look at the case where the two circles in question are drawn so that they are tangent to one another. Form a right triangle with one side joining their centers, one side down the y -axis from the center of the first circle, and a third side oriented horizontally joining the center of the second circle and the y -axis.
The hypotenuse will then have length 2 r and the vertical side will have length r 2 + 4 1 − r . But since the point of tangency is a vertical distance of 2 1 below the center of the first circle, we also know that the vertical side of the triangle has length 2 ∗ 2 1 = 1 . Thus
r 2 − r + 4 1 = 1 ⟹ 4 r 2 − 4 r − 3 = 0 ⟹ ( 2 r − 3 ) ( 2 r + 1 ) = 0 ⟹ r = 2 3 , − 2 1 .
Since r > 0 we must have r = 2 3 , and so a = 3 , b = 2 and a + b = 5 .