Geo-gebra 2
on the given figure, a circle w with centre at O and diameter AB = 2R. inside the circle there are two similar circular arcs of radius R with centres at A,B and they intersect at O.if the green area is H and the area of the circle w is F, then H/F = ( √a – π) / 3π. Find the value of a.
Notation: The two arcs and the diameter AB all intersect at O.

The answer is 27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
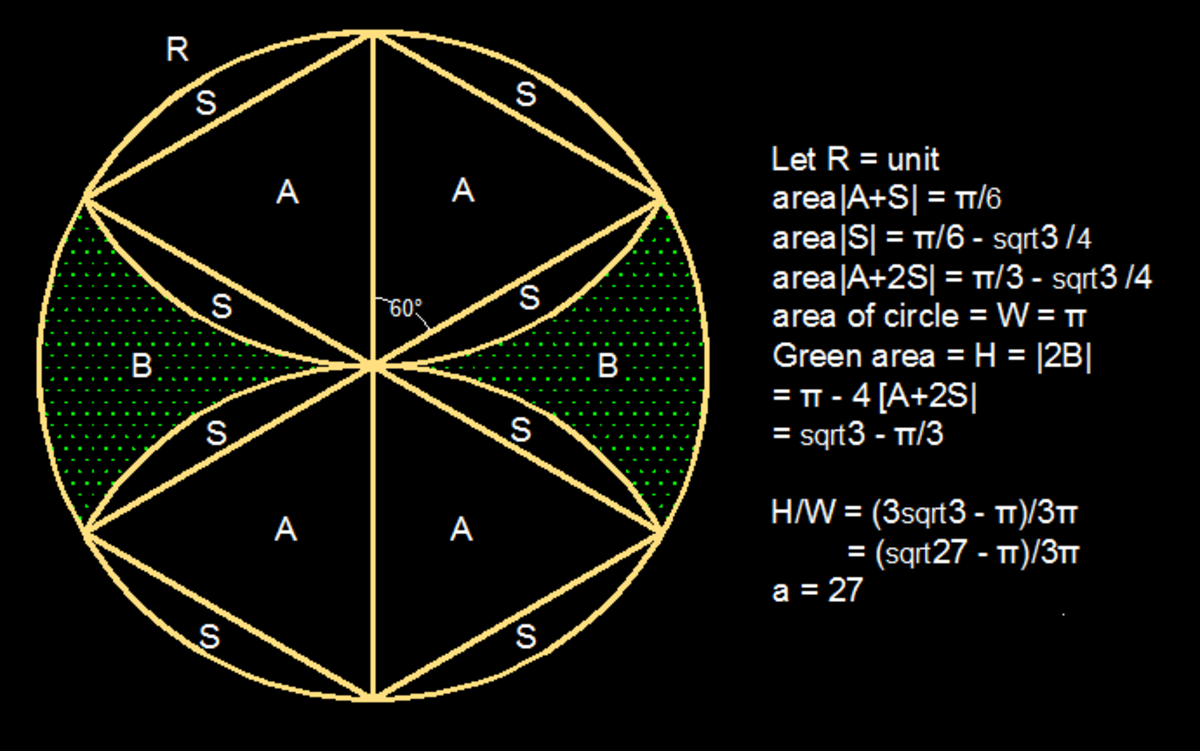
Let the circles centres at O,A,B ,(the radius of All circles is R ) be : (0,0 ) , (0,R ) , (0,-R ) respectively. hence their equations will be : x² + y²=R² , x² + (y-R)² = R² , x² + (y+R)² = R² respectively. Now we can use these equations to determine the points of intersections N,P,M,and Q. From these coordinates we compute the following lengths : NP = MQ = √3R , PQ = NM = R. NMPQ Area = √3R² (rectangle). Area of sectors NOP + MOQ = A1 = 2R²(π/3-√3/4) , Similarly Area of sectors made by NM and PQ = A2 = 2R²(π/6-√3/4) , The green aera H = MNPQ – A1 + A2 = R²(√3-π/3). F = πR² , H/F = (3√3-π)/3π = (√27-π)/3π.