Geo geo
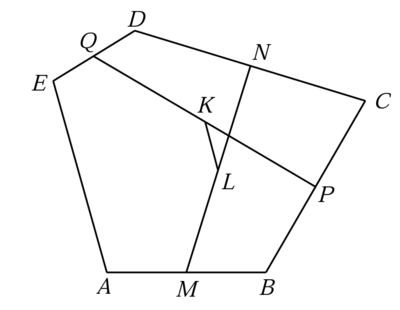
In pentagon A B C D E , points M , P , N and Q are midpoints of A B , B C , C D and D E respectively. While points K and L are midpoints of Q P and M N respectively. If K L = 2 5 , find the length of E A .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the position coordinates of A , B , C , D , E be ( 0 , 0 ) , ( b , 0 ) , ( c 1 , c 2 ) , ( d 1 , d 2 ) , ( e 1 , e 2 ) respectively. Then those of M , N , P , Q , K , L are
( 2 b , 0 ) , ( 2 c 1 + d 1 , 2 c 2 + d 2 ) , ( 2 b + c 1 , 2 c 2 ) , ( 2 d 1 + e 1 , 2 d 2 + e 2 ) , ( 4 b + c 1 + d 1 + e 1 , 4 c 2 + d 2 + e 2 ) , ( 4 b + c 1 + d 1 , 4 c 2 + d 2 ) respectively.
Hence, ∣ K L ∣ = 4 e 1 2 + e 2 2 = 2 5
⟹ ∣ E A ∣ = e 1 2 + e 2 2 = 1 0 0 .
Let a represent the position vector of point A , and so on. From the midpoint conditions on the sides: 2 m 2 p 2 n 2 q = a + b = b + c = c + d = d + e
Similarly, for K and L : 4 k 4 l = 2 p + 2 q = b + c + d + e = 2 m + 2 n = a + b + c + d
Subtracting, 4 ( k − l ) = e − a
Hence E A = ∣ e − a ∣ = 4 ∣ k − l ∣ = 4 K L = 1 0 0 .
Not only that, but the lines K L and E A are parallel.