Trapped Triangles

Geometry Level 3

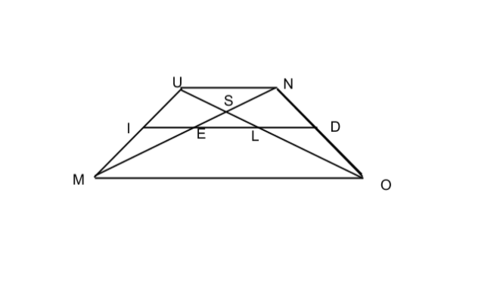In the above figure, line segments UN, DI, and MO parallel, while I and D are the midpoints of UM and NO respectively. If MO = 64, UN = 28, and MN = 46, find ES.


The answer is 9.

Asher Joy by Asher Joy , 22, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Asher Joy
Mar 31, 2014

We know that UNS is similar to SOM: 28/64 = 7/16. MS + SN = 46. Letting x = MS, we get x + 7x/16 = 46, or that MS = 32 and SN = 14. SEL and USN are also similar: Letting EL = y, we get y/28 = SE/14. Finally, END and MNO are also similar: Since ND/DO = 1/2, NE = 1/2 * 46 = 23. ES = NE - SN = 23 - 14 = 9!

14 Helpful 0 Interesting 0 Brilliant 0 Confused

nd:do=1:1 right??? as d is the midpoint of no. it would be nd:no...

sayantan bose - 7 years, 2 months ago

Log in to reply

nd:do is 1:1.

Asher Joy - 7 years, 2 months ago

it was easy

Indrashis Haldar - 7 years, 2 months ago

NDE similar NOM Therefore, ND/NO=ED/MO Therefore, ED=32 Similarly, LD=14 Therefore,EL=ED-LD=18 But, USN similar LSE Therefore, UN/LE=NS/ES=14/9 SO, NS=14ES/9 But, ES+NS=23 (since E is midpoint of MN by BPT) ES+14ES/9 =23 Therefore, ES=9

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Parallel line from mid point means that we have DI is equal to .5(64+28)=32+14=46 and then we have two identical triangularity left and write based on UN and another two based on MNO so we simply by similarity we can find ES to be part of MN by ES =9

0 Helpful 0 Interesting 0 Brilliant 0 Confused

If you draw a perpendicular from N to line MO at point X then doesn't MX become 46? If it does then the right angled triangle MNX can't exist because MX = MN = 46. Could someone clarify please?

Syed Aashir Naqvi - 7 years, 2 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...