Geo-math-trick (Geometry)!

Geometry Level 5

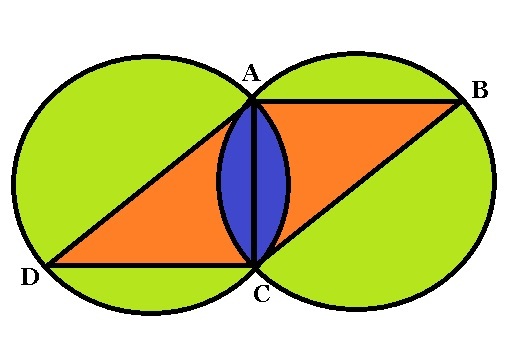
If $\triangle ABC$ and $\triangle ADC$ are Right angled triangle with $\angle DCA=\angle BAC=90^{\circ}$ with $AC$ being the smallest side for each triangle and both the circles have equal diameter of $68$ cm. And each side of both the triangles is an integer.

Then find the minimum area of the blue region in $\text{cm}^{2}$ . Correct your answer to three decimal places before entering it.

The answer is 172.781.

1 solution

Niranjan Khanderia
May 1, 2016

$\text{Let O be the center of circle ADC and M midpoint of AC.}\\ \text{Since 68 is the hypotenuse of right triangle with integer sides we have Pythagorean triple.}\\ \text{ 68=4*17. So the triple is 4*(8-15-17). ..AC=32, DC=60, DA=68, radius=34.}\\ \text{The angle common chord AC substance at the center}\\ \text{= 2* angle ADC=2*ArcTan{AC/DC}=2*ArcTan{32/60}}\\ \text{So the area of sector }AOC =ArcTan(\frac {32}{60})*34^2.\\ Area\ of\ \Delta\ AOC=\frac 1 2 *AC*OM=\frac 1 2 *32*\frac {60} 2.\\ \therefore\ Shaded\ area\ =2*\left (ArcTan(\frac {32}{60})*34^2 - \frac 1 2 *32*\frac {60} 2 \right )=\Large \color{#D61F06}{172.781}$

Nice one.I think it would have been better if you had mentioned why AC=32 & not DC.(To minimize the area.)

rajdeep brahma - 4 years, 2 months ago

What is arctan ?

Mr. India - 2 years, 6 months ago

Wrong solution please make it correct

Aman Vishwakarma - 2 years, 5 months ago

Geo-math-trick (Geometry)!

The answer is 172.781.

1 solution

0 pending reports