Geogebra3
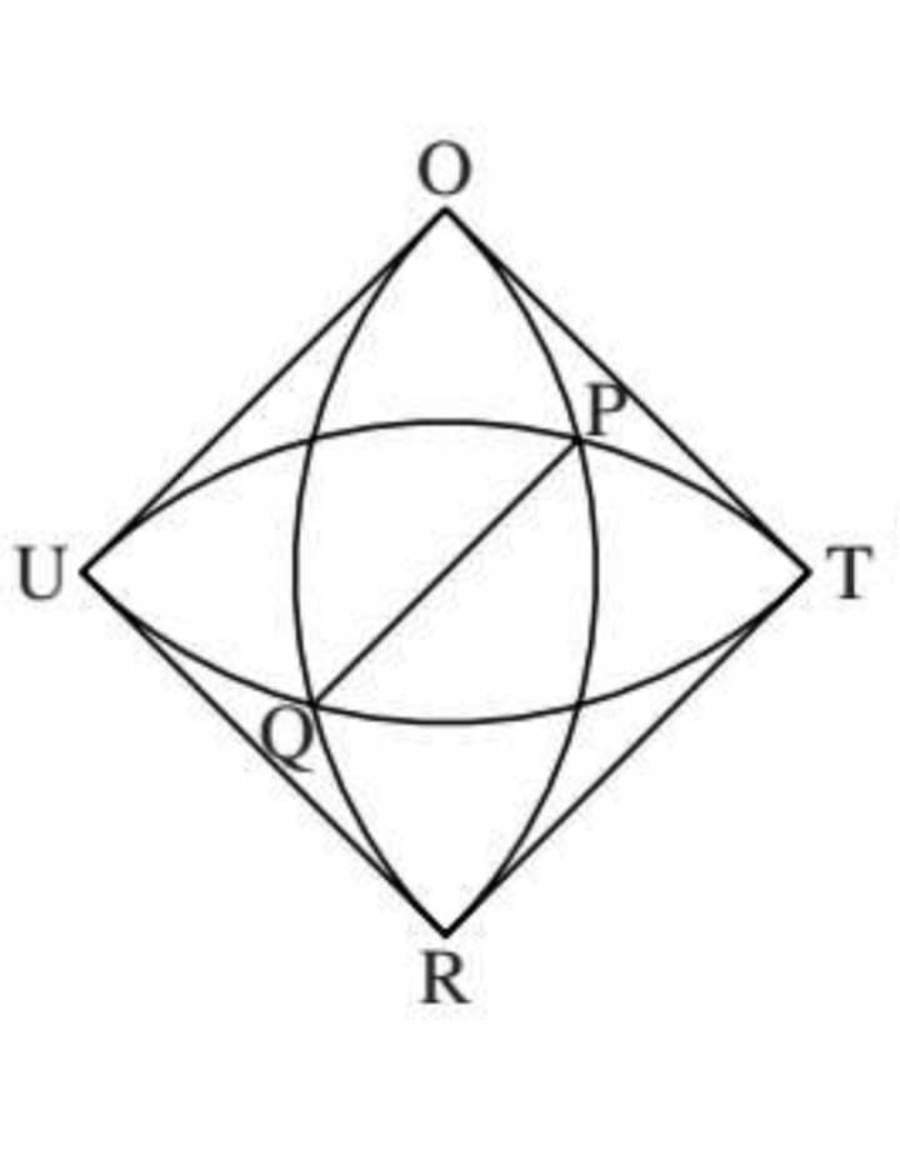
The figure shows a square U R T O of unit side length. If the length of P Q = n − 1 , find n .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
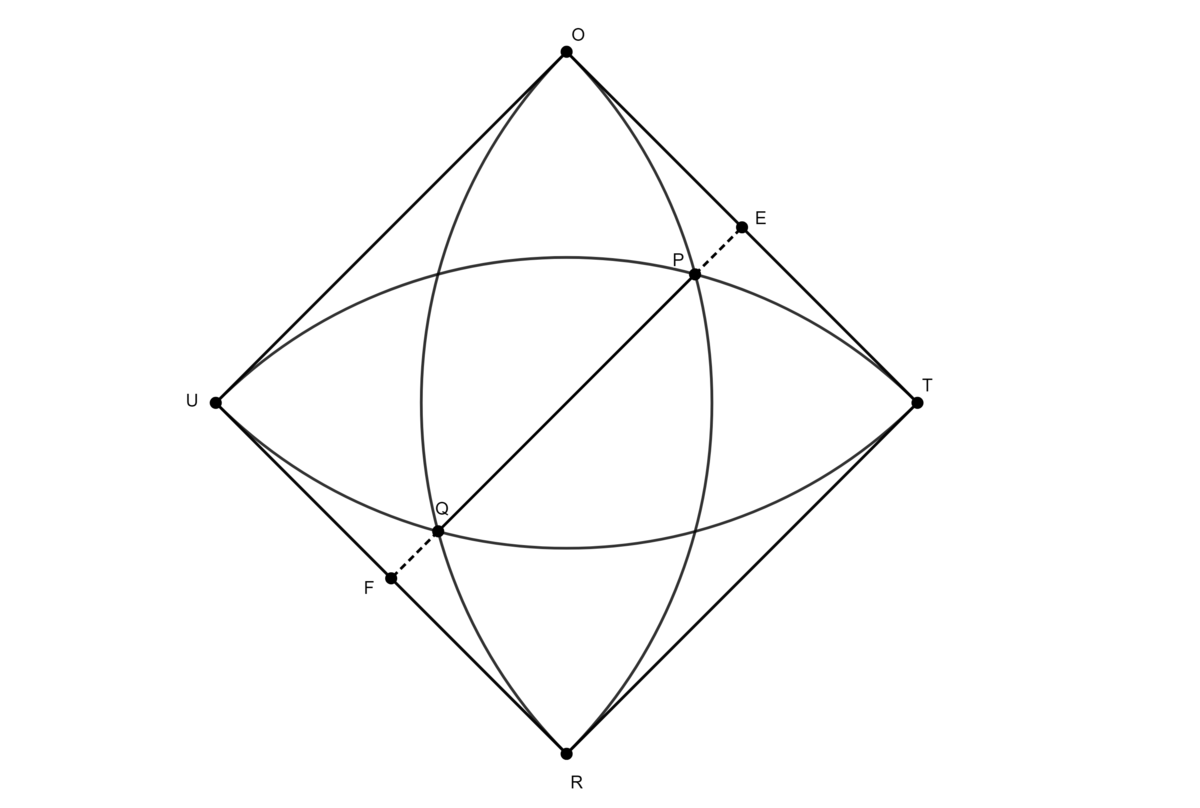 As shown, extend
P
Q
and call its intersections with
O
T
and
U
R
E
and
F
, respectively. By symmetry,
O
E
=
E
T
=
U
F
=
F
R
=
2
1
. Thus
∠
P
U
F
=
cos
−
1
2
1
=
3
π
and
P
F
=
2
3
. Similarly,
Q
E
=
2
3
. Thus
P
Q
=
E
F
−
(
Q
F
)
−
(
P
E
)
=
1
−
2
(
1
−
2
3
)
=
3
−
1
So
n
=
3
.
As shown, extend
P
Q
and call its intersections with
O
T
and
U
R
E
and
F
, respectively. By symmetry,
O
E
=
E
T
=
U
F
=
F
R
=
2
1
. Thus
∠
P
U
F
=
cos
−
1
2
1
=
3
π
and
P
F
=
2
3
. Similarly,
Q
E
=
2
3
. Thus
P
Q
=
E
F
−
(
Q
F
)
−
(
P
E
)
=
1
−
2
(
1
−
2
3
)
=
3
−
1
So
n
=
3
.
Let's place a coordinate system such that U = ( 0 , 0 ) , R = ( 1 , 0 ) . Then, the two quarter circles with respective centers at U and R obviously intersect at x = 2 1 .
The quarter circle around U can be described by the equation y = 1 − x 2 ⇒ y ( 2 1 ) = 1 − ( 2 1 ) 2 = 2 3 .
If we define point S = ( 2 1 , 2 1 ) to be the midpoint of the square, then ∣ ∣ P S ∣ ∣ = 2 3 − 2 1 = 2 3 − 1 .
Now, ∣ ∣ P Q ∣ ∣ is just twice as long as ∣ ∣ P S ∣ ∣ , so ∣ ∣ P Q ∣ ∣ = 3 − 1 , which makes the answer 3 .
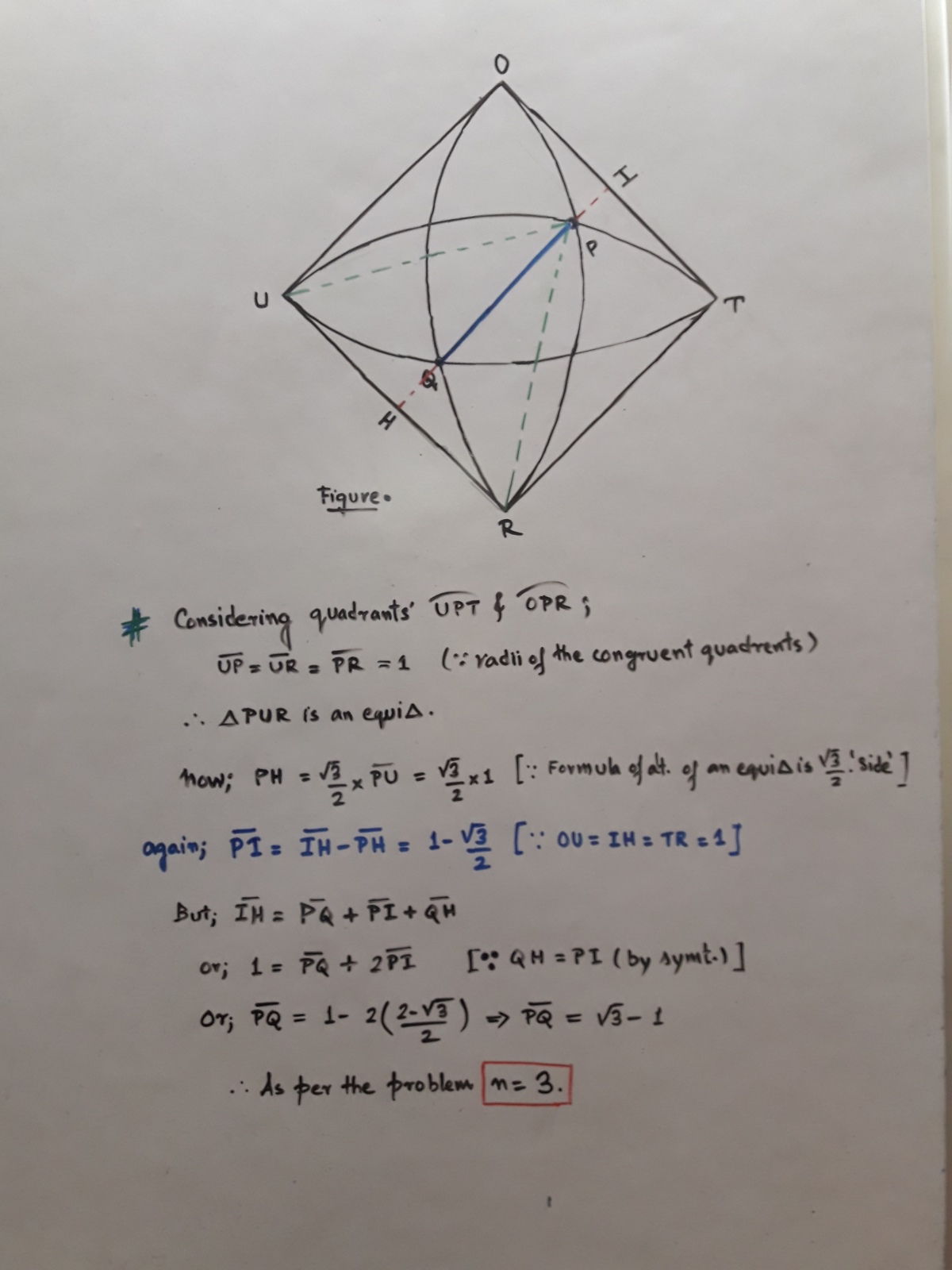
Let the extension of P Q to meet O T and U R at M and N respectively. We note both △ P R U and △ O Q T are both unit equilateral triangles. Therefore, P N = 2 3 , Q N = 1 − 2 3 , and P Q = P N − Q N = 2 3 − ( 1 − 2 3 ) = 3 − 1 . Implying n = 3 .