Geom is fun... :)
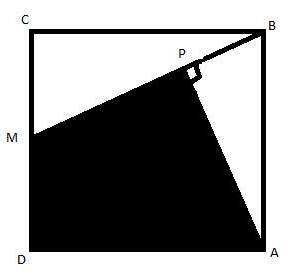 Square ABCD has side 1. M is the midpoint of [CD]. Angle APB is 90 degrees. Find the area of the shaded region.
Square ABCD has side 1. M is the midpoint of [CD]. Angle APB is 90 degrees. Find the area of the shaded region.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Log in to reply
Did the same way! :D By d way, is there a shorter one?
Log in to reply
Probably, haha.
yes there is ...i'll tell u ..use co-ordinate axes ...take origin at D ..... find the equation of line BM u will get as x-2y=-1 ..also now we need to find the equation of the line AP to get the co-ordinate of the point P... since AP is perpendicular to BM its slope is 1/2 and line AP passes through (0,1) therefore the equation of the line is 2x+y=1 and P(1/5,3/5) ....now find the distance of AP and BP by diatance formula which will come as AP=1/sqrt[5] and BP=2/sqrt[5].... now find the areas of the two triangle BCM and APB ... at last u will do 1-1/4-1/5=11/20...
What are the similarity criterions ? Could u tell me the full list ?
Find the areas of both triangles and the square then subtract it from the sum of the areas of triangles. ........that's how I got it
BM = (square root of 5 )/2
area of triangle ABM = 0.5 BM.AP
AP = 2/(square root of 5)
PB = 1/(square root of 5)
area of triangle APB = 1/5
area of triangle BCM = 1/4
area of the shaded region = 1 - 1/4 - 1/5 = 11/20
CM =1 so area of triangle CMB is 1/4. Area of square is 1. Now area of ABCD- Area of CMB is 3/4. Therefore area of shaded region is less than 3/4. If you see the last 2 answer choices are greater than 3/4 . Eliminate answer choice D and E. Visually we can see PB is almost equal to CM and lets assume PB =1/2. Now using pytho we can find area of triangle APB is approx (sqrt3)/8 . so shaded area = 3/4 -(sqrt3/8) = approx half which is answer choice A :-) Not the most elegant way but fastest as far as I know.
There's a much better way to do it, but since I don't remember much geometry, I used repeated applications of law of sines to find the exact values of BP and PA. Eventually, you get 1 − 4 1 − 5 1 = 2 0 1 1
M is midpoint so CM = 1/2(CD)=1/2 (CB) hence angle CMB = 60 degrees angle CBP = 30 degrees angle CMB = 60 degrees Angle PBA = 60 degrees Area of triangle BPMCB = 1/2 (CM x CB) = 1/4(CB x CB) = 1/4 units
Sin(theta)=BP/BA Now Cos (theta)=PA/BA
Are of Triangle BPAB = 1/2 (BP xPA)= 1/2 ( √3/2 x 1/2)= √3/8 units
shaded area = 1 sq unit - ((1/4)+√3/8 ) = 11/20 units
how come angle CMB=60 degree if CM=0.5CB for triangle CMB , S i n ( ∠ C M B ) = C B / B M = 1 / ( 5 / 2 ) = 2 / 5 . H e n c e ∠ C M B i s n o t 6 0 d e g r e e
Log in to reply
Absolutely Abhiram ..Mr. Iqbal did it wrongly
Let N be the point in BM...
So, BM = V(1+1/4) = V(5/4) = (V5)/2
So, let BN = x
Then, NM = [(V5)/2] - x
AN = V(1 - x^2)
So,
a^2 + b^2 = c^2
(V(1-x^2))^2 + (((V5)/2)-x))^2 = (V(1+1/4))^2
(1-x^2) + (5/4 - x(V5) + x^2) = 5/4
1 = x(V5)
(V5)/5 = x
MN = 3(V5)/10
AN = 2(V5)/5
So, area of shaded region = Area of (ANM) + Area of (AMD)...
= [3(V5)/10 * 2(V5)/5]/2 + [1/2]/2
= (3/5 + 1/2)/2
= (11/10)/2
= 11/20 sq. Units...
It is taking long time to solve this.
if u r good at geometry...it is easily visible that the area of shaded region will be less than (3/4) and greater than (1/2)...and there is only one option which satisfies that.
We note A B / / M C → ∠ A B P = ∠ B M C and ∠ A P B = ∠ B C M ; due to the AA similarity criterion,
Δ A B P ∼ Δ B M C
By Pythagoras' Theorem,
B M = C M 2 + C B 2 = ( 2 1 ) 2 + 1 2 = 2 5
Using the properties of similarity,
P B = B M A B × C M = 5 / 2 1 × 2 1 = 5 1
P A = B M A B × C B = 5 / 2 1 × 1 = 5 2
The area of Δ A B P and Δ B M C are, respectively,
Δ A B P = 2 1 × P B × P A = 2 1 × 5 1 × 5 2 = 5 1
Δ B M C = 2 1 × C M × C B = 2 1 × 2 1 × 1 = 4 1
Following that, we evaluate the area of the square:
A s q u a r e = s 2 = 1 2 = 1
Finally, the shaded region is then the square minus the two triangles:
A s h a d e d r e g i o n = A s q u a r e − Δ A B P − Δ B M C = 1 − 5 1 − 4 1
= 2 0 1 1