geometras 4 all

Geometry Level 3

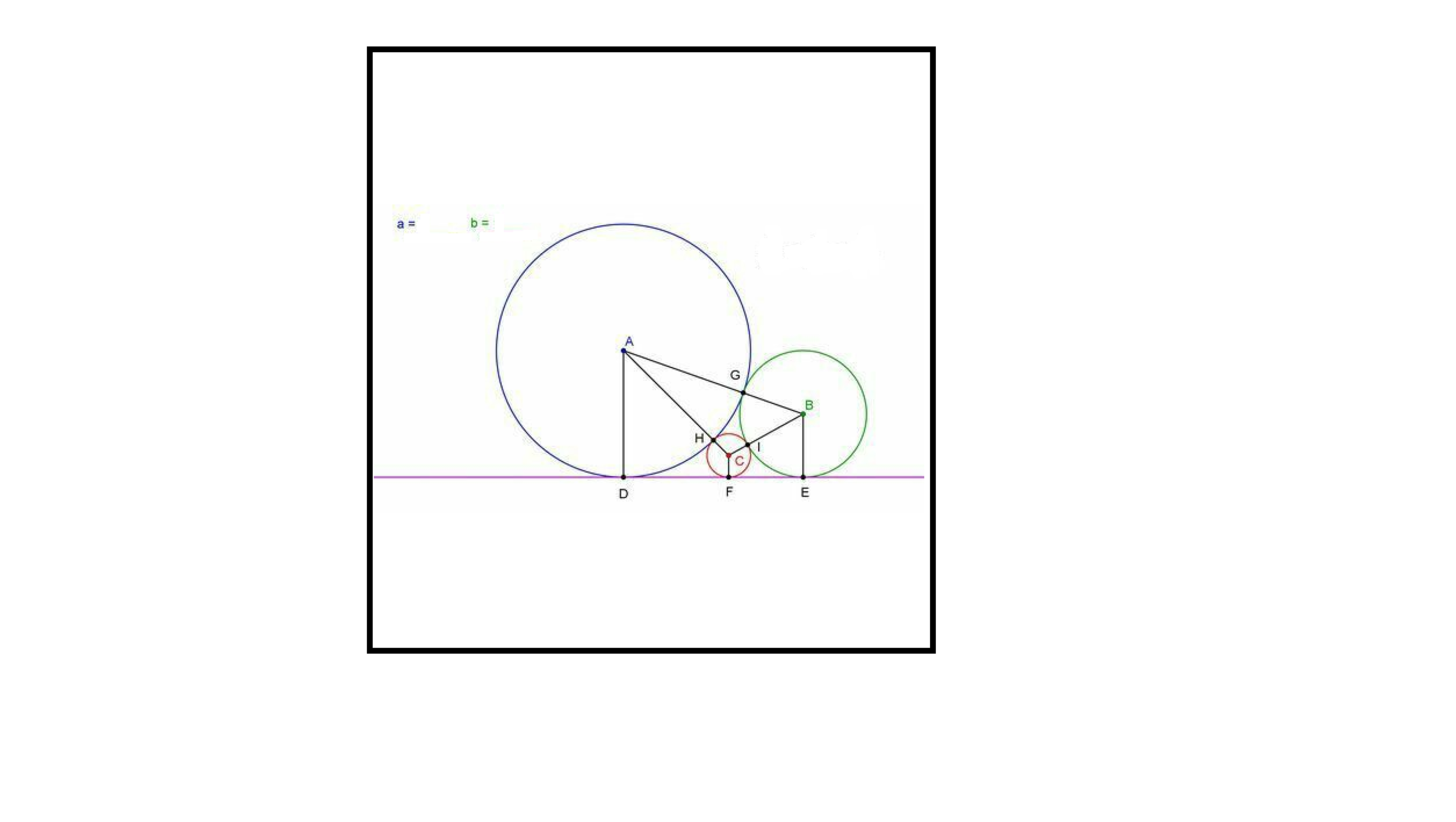
The figure shows two circles of different radii, the circle with centre at A has radius r =a, the circle with centre at B has

radius r = b , The two circles are tangential to each other at point G. there is another small circle with centre at C and

radius r = c which is in turn tangential to both circles at points H and I , the three circles are all tangential to the line DFE .

find the value of c in terms of a and b .

If a = 16 , b = 9 , then c = m n \frac{m}{n} , where m and n are positive integers , find m + 16 n − 41 \frac{m +16}{n - 41} .


The answer is 20.

Aziz Alasha by Aziz Alasha , 59, Sudan

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Arjen Vreugdenhil
Dec 12, 2017

We will solve the problem in general. Let p = D F p = DF and q = F E q = FE .

The segment A B = a + b AB = a + b may be viewed as the hypotenuse of a right triangle with width p + q p + q and height a − b a - b . Pythagoras gives ( a + b ) 2 = ( a − b ) 2 + ( p + q ) 2 ∴ ( p + q ) 2 = 4 a b , p + q = 2 a b . (a+b)^2 = (a - b)^2 + (p+q)^2\ \ \ \ \therefore\ \ \ \ (p+q)^2 = 4ab,\ \ p + q = 2\sqrt{ab}. Applying a similar strategy to A C AC and B C BC , we obtain ( a + c ) 2 = ( a − c ) 2 + p 2 ∴ p 2 = 4 a c , p = 2 a c ; (a+c)^2 = (a - c)^2 + p^2\ \ \ \ \therefore\ \ \ \ p^2 = 4ac,\ \ p = 2\sqrt{ac}; ( b + c ) 2 = ( b − c ) 2 + q 2 ∴ q 2 = 4 b c , q = 2 b c . (b+c)^2 = (b - c)^2 + q^2\ \ \ \ \therefore\ \ \ \ q^2 = 4bc,\ \ q = 2\sqrt{bc}. Now ( p + q ) 2 = p 2 + q 2 + 2 p q ; (p+q)^2 = p^2 + q^2 + 2pq; 4 a b = 4 a c + 4 b c + 8 a b c = 4 c ( a + b ) 2 ; 4ab = 4ac + 4bc + 8\sqrt{ab}c = 4c\left(\sqrt a + \sqrt b\right)^2; c = a b ( a + b ) 2 . c = \frac{ab}{\left(\sqrt a + \sqrt b\right)^2}.

With the given values, c = 16 ⋅ 9 ( 4 + 3 ) 2 = 144 49 ; c = \frac{16\cdot 9}{(4 + 3)^2} = \frac{144}{49}; we submit the value of 144 + 16 49 − 41 = 160 8 = 20 . \frac{144+16}{49 - 41} = \frac{160}{8} = \boxed{20}.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...