Geometric Application of Trigonometry 1

Let $\angle BAM = \alpha$ ; then $\sin \alpha = \frac 13$ . Let $\angle BAC = \theta$ and we need to find $\sin \theta$ . Let $AC =b$ . From the figure above, we have $\begin{cases} \tan \theta = \dfrac 2b \\ \tan (\theta - \alpha) = \dfrac 1b \end{cases}$

$\begin{aligned} \implies \tan \theta & = 2 \tan (\theta - \alpha) \\ & = \frac {2(\tan \theta - \tan \alpha)}{1+\tan \theta \tan \alpha} & \small \color{#3D99F6} \text{As }\sin \alpha = \frac 13 \implies \tan = \frac 1{2\sqrt 2} \\ & = \frac {2\left(\tan \theta - \frac 1{2\sqrt 2} \right)}{1+ \frac 1{2\sqrt 2}\tan \theta} \\ & = \frac {4\sqrt 2 \tan \theta - 2}{2\sqrt 2+ \tan \theta} \end{aligned}$

$\begin{aligned} \implies \tan^2 \theta - 2\sqrt 2 \tan \theta + 2 & = 0 \\ (\tan \theta - \sqrt 2)^2 & = 0 \\ \tan \theta & = \sqrt 2 \\ \implies \sin \theta & = \frac {\sqrt 2}{\sqrt 3} = \boxed{\frac {\sqrt 6}3} \end{aligned}$

Let $a = BC$ (so that $\frac{1}{2}a = CM = BM$ ), $b = AC$ , $c = AB$ , and $m = AM$ .

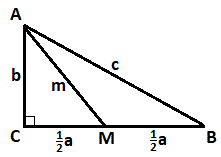
The area of $\triangle BAM$ can be expressed as $A_{\triangle BAM} = \frac{1}{2}mc \sin (\angle BAM) = \frac{1}{6}mc$ and $A_{\triangle BAM} = \frac{1}{2} \cdot \frac{1}{2}a \cdot b = \frac{1}{4}ab$ . Equating the two area equations and simplifying gives $2mc = 3ab$ .

By Pythagorean's Theorem on $\triangle ACM$ and on $\triangle ABC$ we have $m = \sqrt{\frac{1}{4}a^2 + b^2}$ and $b = \sqrt{c^2 - a^2}$ . Substituting these into $2mc = 3ab$ gives $2c \sqrt{\frac{1}{4}a^2 + (c^2 - a^2)} = 3a\sqrt{c^2 - a^2}$ , which solves to $a = \frac{\sqrt{6}}{3}c$ .

Therefore, $\sin \angle BAC = \frac{a}{c} = \boxed{\frac{\sqrt{6}}{3}}$ .

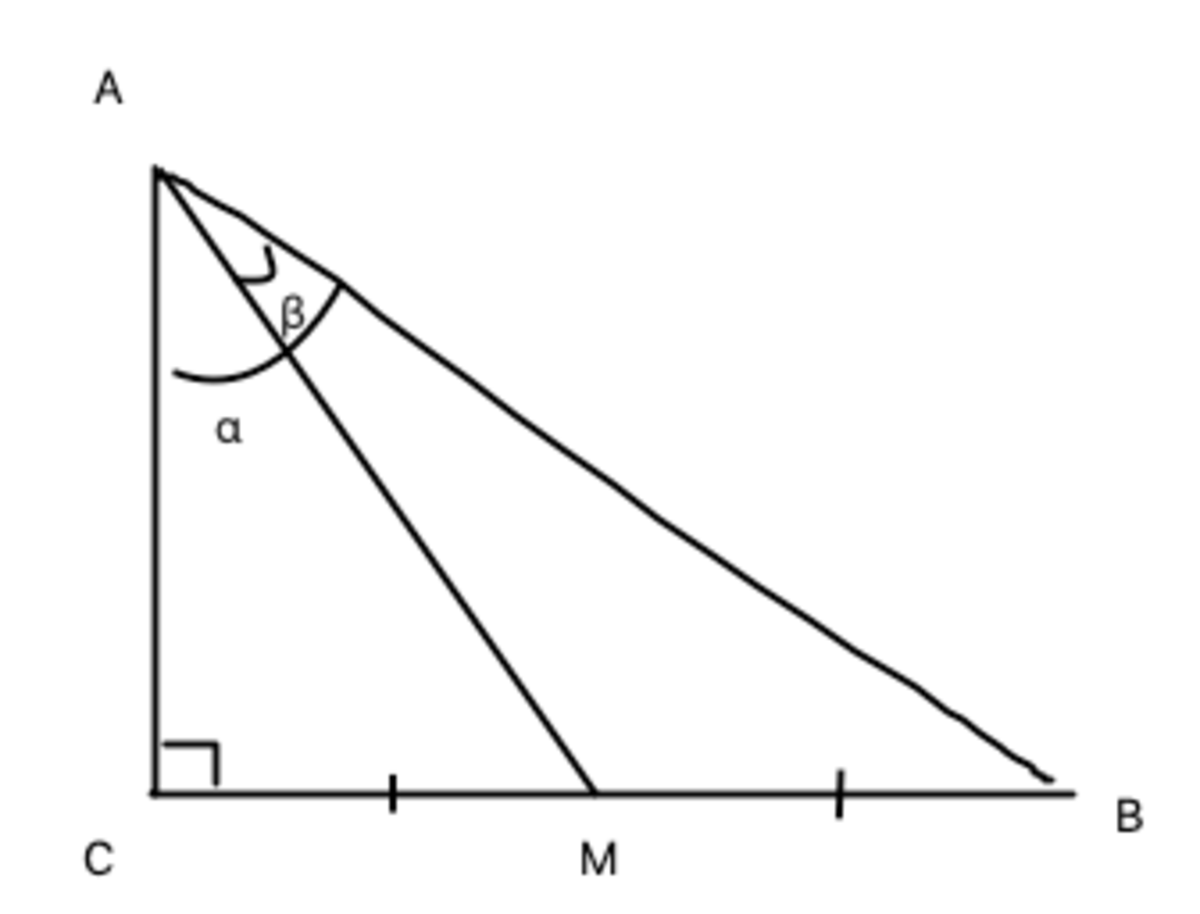
Let $\angle BAM = β$ $\angle BAc= α$ $\\$ Thus $CM = AM \sin(α - β)$ $\\$ $\\$

$\because$ $M$ is the mid-point of $BC$ $\\$ $\therefore$ $BM = AM \sin(α - β)$ $\\$ $\\$

Using Sine Law on $\triangle AMB$ and get $\frac {AM}{\sin B}=\frac {BM}{ \sin(β)}$ $\\$ Which is $\frac {AM}{\sin (\pi\2 - α)}=\frac {AM \sin(α - β)}{ \sin(β)}$ $\\$ $\\$

$\because$ $\sin(β)$ = $\frac{1}{3}$ $\\$ $\therefore$ $\cos(β)$ = $\frac{2 \sqrt {2}}{3}$ $\\$ $\therefore$ $\frac{1}{3} = \cos (α) (\frac{2 \sqrt {2}}{3} \sin (α) - \frac{1}{3} \cos (α)$ = $\frac{2}{3} \sqrt {2} \sin (α) \cos (α) - \frac{1}{3} \cos ^{2} (α)$ $\\$ $1 = 2\sqrt {2} \sin (α) \cos (α) - \cos ^{2} (α)$ (Divide $\cos^{2} (α)$ on both sides) $\\$ $\\$ $\tan (α) = \sqrt 2$ $\\$ $\sin (α) = \frac {\sqrt 6}{3}$ $\\$