Geometric Concept

Geometry Level 3

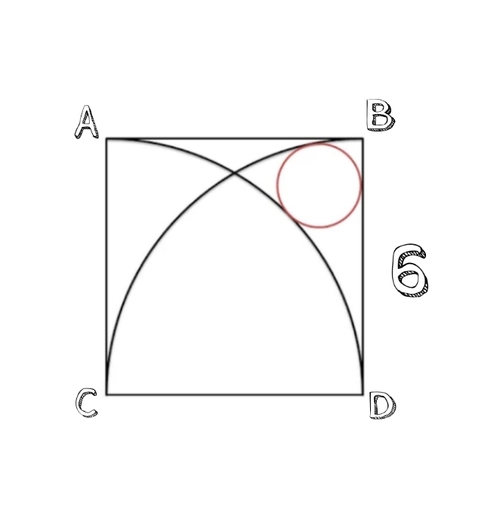ABCD is a square. The length of the side is 6. Find the radius of the smaller circle.


The answer is 1.00.

View wiki
Vedant Yadav by Vedant Yadav , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Discussions for this problem are now closed

Let P be the center of the small circle. L e t P M ⊥ B D , P N ⊥ C D Let~~PM \perp BD~~, PN \perp CD and r the radius of the small circle. For tangential contacts, P D = 6 − r , C P = 6 + r , P M = r . P N = M D s i d e s o f t h e r e c t a n g l e P M D N , ∴ N D = r , C N = 6 − r . I n r i g h t e d △ s C P N a n d D P M , C P 2 − C N 2 = P N 2 = M D 2 = P D 2 − P M 2 , ⟹ ( 6 + r ) 2 − ( 6 − r ) 2 = ( 6 − r ) 2 − r 2 , ⟹ 36 r = 36 ; r = 1 P D = 6 - r, ~~~~~~ CP = 6 + r, ~~~~~~ PM = r. \\PN = MD~sides ~of ~the~ rectangle~PMDN ,\\\therefore~ND = r, ~~~~CN = 6 - r.\\ In~~righted~\bigtriangleup s~~~~CPN~~and~~DPM,\\ CP^2-CN^2 = PN^2 = MD^2 = PD^2 -PM^2,\\\implies~(6 + r)^2-(6 - r)^2 = (6 - r)^2-r^2, \\\implies~36r = 36;~~~~~~ ~~r = \boxed{ 1 }
I am adding this note for better understanding. :- C is center of arcs AD with radii CA and CD =6. .......D is center of arcs CB with radii DC and DB =6.

24 Helpful 0 Interesting 0 Brilliant 0 Confused

Can you please tell me how we assumed C,P and the tangential point on the arc AD to be collinear? Coz unless they are collinear, CP can't be equal to '6+r'.

Anshul Toshniwal - 6 years, 5 months ago

Line joining two centers of circular arc (C and P here), passes through the point of tangency. I hope this will be satisfactory.

Niranjan Khanderia - 6 years, 5 months ago

If PN ⊥ CD so,why can't i use : CP² = CN * CD ?

Race mica - 6 years, 5 months ago

how can u take PD as 6cm? 'cause BD is 6cm not PD

Chethashree Chandrashekar - 6 years, 5 months ago

Notice that P D PD is also a section of the radius of one of the bigger quarter circles. Let Q Q be on the bigger quarter circle such that Q D QD passes through P P and is the radius of that bigger quarter circle. QP is the radius of the small circle as he said. We know that Q P + P D = Q D = 6 QP+PD=QD=6 (the radius of the bigger quarter circle is equal to the side of the square). Q P = r QP = r so P D = 6 − r PD =6-r

William Isoroku - 6 years, 5 months ago

Thanks for the explanation.

Niranjan Khanderia - 6 years, 5 months ago

I have said PD= 6 - r. William Isoroku below has explained this.

Niranjan Khanderia - 6 years, 5 months ago
Chew-Seong Cheong
Dec 17, 2014

Let the center of the smaller circle be O ( x , y ) O\space (x,y) its radius r r . Then ( x , y ) (x,y) satisfy the following equations:

{ x 2 + y 2 = ( 6 + r ) 2 . . . ( 1 ) ( x − 6 ) 2 + y 2 = ( 6 − r ) 2 . . . ( 2 ) x = 6 − r . . . ( 3 ) \begin {cases} x^2 + y^2 = (6+r)^2 &... (1) \\ (x-6)^2 + y^2 = (6-r)^2 &...(2) \\ x = 6 - r &...(3) \end {cases}

Equation 1 - equation 2: ⇒ 12 x − 36 = 24 r ⇒ x − 3 = 2 r \Rightarrow 12x - 36 = 24r \quad \Rightarrow x - 3 = 2r

Substituting x = 6 − r ⇒ 6 − r − 3 = 2 r ⇒ r = 1 x = 6-r \quad \Rightarrow 6 - r - 3 = 2r \quad \Rightarrow r = \boxed {1}

8 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...