Geometric Geometry
If the lengths of sides A B , B C and A C in the figure shown form a geometric progression in that order, what is the ratio between A C and A B to 3 decimal places?
The answer is 1.618.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The Golden Ratio pops up once again !!
Is it possible to determine the value of each side?
Log in to reply
For a given value a > 0 the side lengths would be a , a r , a r 2 , where
r = 2 1 + 5 ≈ 1 . 2 7 2 .
So, for example, if a = 3 then the side lengths would be (approximately)
3 , 3 . 8 1 6 , 4 . 8 5 4 , not too far from a 3 / 4 / 5 triangle.
I thought it's suppose to be ratio between AC and AB so shouldnt we need to square the answer?
Log in to reply
Since ∣ A B ∣ = a and ∣ A C ∣ = a r 2 the ratio will be ∣ A B ∣ ∣ A C ∣ = r 2 , which has been calculated.
Log in to reply
oh ok thanks for the reply lol i missed that
I've done something very similar but I'm having a hard time understanding why mine is wrong.
Since the 3 side lengths are a geometric sequence, we can say
x^2 + ax^2 = a^2x^2
divide everything by x^2
1+a=a^2
a = golden ratio.
since ratio between AC and AB is (a^2x^2/x^2), which is a^2, shouldn't the answer be the golden ratio squared? I really don't know where I messed up in my solution.
B
C
A
B
=
A
C
B
C
tan
(
C
)
=
cos
(
C
)
sin
(
C
)
=
cos
2
(
C
)
=
1
−
sin
2
(
C
)
sin
(
C
)
>
0
so
sin
(
C
)
=
2
−
1
+
√
5
Answer is sin ( C ) 1 = 5 − 1 2 = 2 5 + 1 ≈ 1 . 6 1 8
Your trigonometric solution is pretty unique, other solutions reduced it to algebraic form and solve them.
I've formatted your solution with L a T e X so it would be more attractive and easier to follow. Hopefully, it gets more views as well!
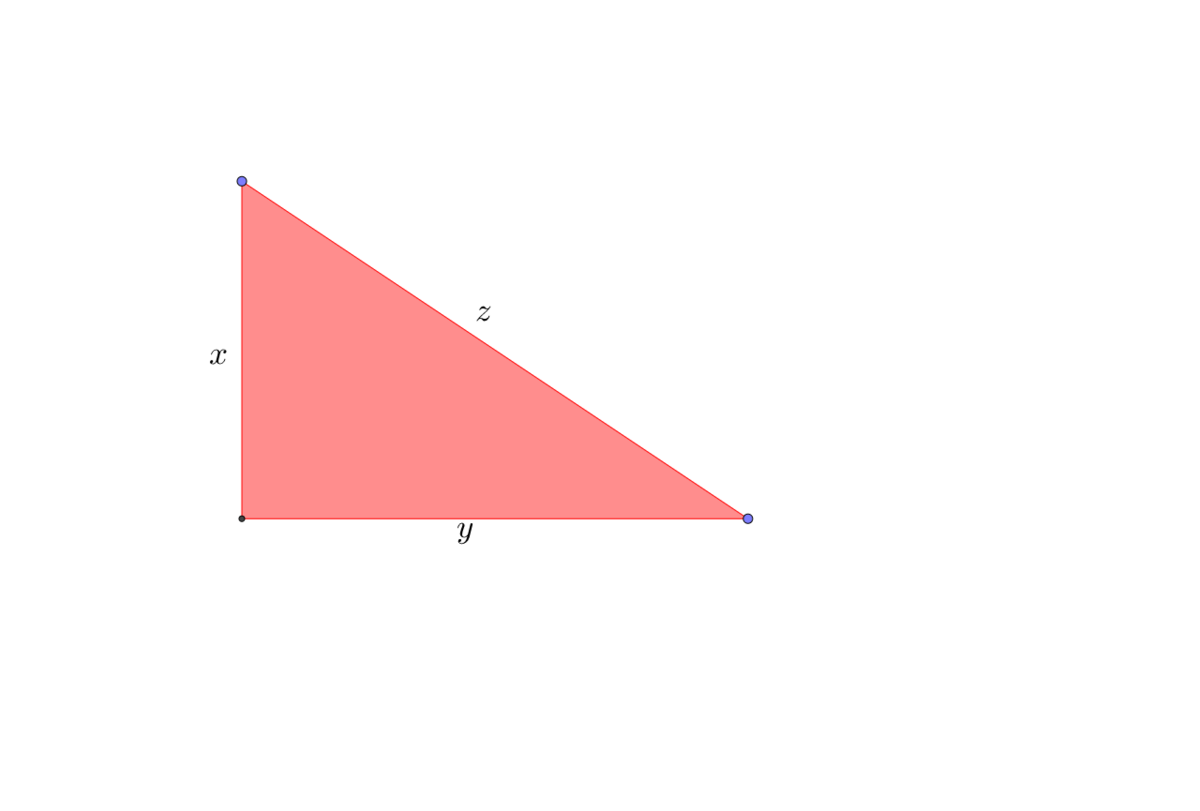
let x , y , z denote the sides of the triangle with x < y < z
By Pythagoras theorem we have, x 2 + y 2 = z 2
Also, since x,y,z are in G.P we have y 2 = x z
Thus we get, x 2 + x z = z 2
or, ( x z ) 2 − x z − 1 = 0
on solving we get, x z = 2 1 ± 5
however since x , y , z > 0 we have x z = 2 1 + 5 = 1 . 6 1 8
Since Δ A B C is right angled we know that A C is the longest side, so we can let the progression ∣ A B ∣ , ∣ B C ∣ , ∣ A C ∣ be a , a r , a r 2 for some reals a > 0 , r > 1 . Then by Pythagoras we have that
∣ A C ∣ 2 = ∣ A B ∣ 2 + ∣ B C ∣ 2 ⟹ ( a r 2 ) 2 = a 2 + ( a r ) 2 ⟹ a 2 ( r 4 − r 2 − 1 ) = 0 .
As a = 0 we must then have that r 4 − r 2 − 1 = ( r 2 ) 2 − r 2 − 1 = 0 , and thus that
r 2 = 2 1 ± 5 . As r 2 is necessarily positive we take the positive root as the answer, i.e.,
r 2 = 2 1 + 5 = 1 . 6 1 8 to 3 decimal places.