Is This Another Triangle Inequality?

Geometry Level 4

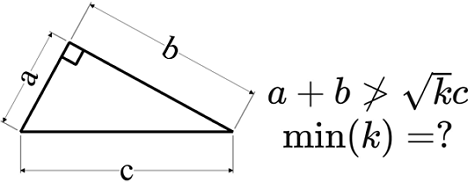
Find the smallest k k such that the sum of the legs of a right triangle never exceeds k \sqrt{k} times the hypotenuse of the triangle.

Give your answer to 3 decimal places.


The answer is 2.

View wiki
A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

5 solutions

Hung Woei Neoh
Jun 3, 2016

Relevant wiki: Solving Triangles - Problem Solving - Medium

Let the legs of a triangle be a a , b b and the hypotenuse be c c

We are looking for the smallest k k such that

a + b ≤ k c ( a + b ) 2 ≤ ( k c ) 2 a 2 + 2 a b + b 2 ≤ k c 2 a 2 + 2 a b + b 2 ≤ k ( a 2 + b 2 ) k ( a 2 + b 2 ) − a 2 − b 2 ≥ 2 a b ( k − 1 ) ( a 2 + b 2 ) ≥ 2 a b a+b \leq \sqrt{k}c\\ (a+b)^2 \leq (\sqrt{k}c)^2\\ a^2+2ab+b^2 \leq kc^2\\ a^2+2ab+b^2 \leq k(a^2+b^2)\\ k(a^2+b^2) -a^2-b^2 \geq 2ab\\ (k-1)(a^2+b^2) \geq 2ab

Now, since a 2 > 0 , b 2 > 0 a^2 > 0,\;b^2 > 0 , from AM-GM:

a 2 + b 2 2 ≥ a 2 b 2 a 2 + b 2 ≥ 2 a b \dfrac{a^2+b^2}{2} \geq \sqrt{a^2b^2}\\ a^2+b^2 \geq 2ab

Therefore,

( k − 1 ) ( a 2 + b 2 ) − ( a 2 + b 2 ) ≥ 2 a b − 2 a b ( k − 2 ) ( a 2 + b 2 ) ≥ 0 k − 2 ≥ 0 k ≥ 2 (k-1)(a^2+b^2) -(a^2+b^2) \geq 2ab - 2ab\\ (k-2)(a^2+b^2) \geq 0\\ k-2 \geq 0\\ k \geq 2

The smallest natural number of k = 2 k=\boxed{2}

15 Helpful 0 Interesting 0 Brilliant 1 Confused

that was cool

abhishek alva - 5 years ago

I think there is a mistake.if a>b and c> b then a-c is not necessarily greater than 0

firoz khan - 5 years ago

(k-1)(a/b +b/a)≥2 is true for k-1≥1

firoz khan - 5 years ago

I have it similar, but after k-1>=2ab/(a^2 +b^2), I replaced it with 2ch/c^2, with h as the height. And since h<=c/2 (Thales) it gives you k-1>= 2 c 1/2*c / (c^2) =1 => k>=2

Bibin Muttappillil - 5 years ago

You subtracted the second equation from the first. If we subtract the first from the second, we get k ≤ 2 k \leq 2 which is reverse of what you tried to prove.

Atomsky Jahid - 1 year, 1 month ago
Atomsky Jahid
Jun 14, 2016

The square of a real number is always greater than zero. 0 ≤ ( a − b ) 2 0 \leq (a-b)^2 ⟹ 2 a b ≤ a 2 + b 2 \implies 2ab \leq a^2+b^2 So, ( a + b ) 2 = a 2 + b 2 + 2 a b ≤ a 2 + b 2 + a 2 + b 2 (a+b)^2=a^2+b^2+2ab \leq a^2+b^2+a^2+b^2 ⟹ ( a + b ) 2 ≤ 2 ( a 2 + b 2 ) \implies (a+b)^2 \leq 2(a^2+b^2) ⟹ a + b ≤ 2 c \implies a+b \leq \sqrt{2}c Here, the equality happens when a = b a=b .

Now, we have to find k k such that the following inequality is satisfied. a + b ≤ k c a+b \leq \sqrt{k}c k ≥ 2 k \geq 2 satisifies the above inequality. So, m i n ( k ) = 2 min(k) = 2

1 Helpful 1 Interesting 2 Brilliant 0 Confused

He/She asked for min(k) value. You found out max value. 😐

Debasish Roy - 1 year, 1 month ago

Log in to reply

I calculated the max value of m m , not k k . I added a few lines for further clarity. We were asked to find the minimum k k such that the inequality a + b ≤ k c a+b \leq \sqrt{k}c holds. As we can see, k k can be anything greater than 2 2 . So, the minimum value of k k is 2 2 .

Atomsky Jahid - 1 year, 1 month ago

We shall claim that the answer is 2.

Now, let us attempt to prove it.

Let a a be the length of one leg of the triangle, b b be the length of the other leg of the triangle, and a 2 + b 2 \sqrt{a^2+b^2} be the length of the hypotenuse. Hence, we have to prove: a + b ≤ 2 a 2 + 2 b 2 a+b\leq \sqrt{2a^2+2b^2} ⇔ a 2 + b 2 + 2 a b ≤ 2 a 2 + 2 b 2 \Leftrightarrow a^2+b^2+2ab\leq2a^2+2b^2 ⇔ a 2 + b 2 − 2 a b ≥ 0 \Leftrightarrow a^2+b^2-2ab\geq0 ⇔ ( a − b ) 2 ≥ 0 \Leftrightarrow (a-b)^2\geq0 This is obviously true, hence 2 is a possible value.

Obviously 1 is impossible, since triangle inequality is violated.

Thus, the smallest value of k k is 2.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

k need not be an integer, so the last part of your proof is invalid. However, it is easy to see that when a=b, a+b=root(2)c, so clearly no smaller k is possible.

Joe Mansley - 2 years, 9 months ago

I don't know what you guys are doing so I tried a more simplified approach: Set a=3 and b=4 (3-4-5 triangle). Then we'll get 1.96 <= k. So the answer might be 2. Turns out luck is on my side :))

0 Helpful 0 Interesting 0 Brilliant 0 Confused

One way to solve it is to maximize the hypotenuse. For a given total length of two legs, hypotenuse will be greatest when the two legs are equal.

Atomsky Jahid - 4 years, 12 months ago
Akash Shukla
Jun 6, 2016

a + b ≤ k ∗ c a+b≤\sqrt k*c ,

Squaring on both the sides,

a 2 + b 2 + 2 a b ≤ k ∗ c 2 a^2+b^2+2ab ≤ k*c^2

2 a b ≤ ( k − 1 ) c 2 2ab≤(k-1)c^2

k − 1 ≥ 2 a ∗ b c 2 k-1 ≥ 2\dfrac{a*b}{c^2}

k − 1 ≥ 2 s i n ( A ) ∗ s i n ( B ) s i n ( C ) 2 k-1 ≥2\dfrac{sin(A)*sin(B)}{{sin(C)}^2}

k − 1 ≥ 2 s i n ( A ) ∗ c o s ( A ) 1 k-1 ≥2\dfrac{sin(A)*cos(A)}{1} ... ( A = π 2 − B , s i n ( c ) = s i n ( π 2 ) = 1 ) ( A=\dfrac{\pi}{2}-B, sin(c) = sin(\dfrac{\pi}{2}) = 1) ,

k − 1 ≥ s i n ( 2 A ) k-1 ≥sin(2A) ,

k ≥ 1 + s i n ( 2 A ) k ≥ 1+sin(2A)

If my method is right, then min(k) will depend on either of angle A A or B B

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Since A is in between 0 to pi/2, 0< sin(2A) <=1; How would you conclude?

Tarikul Islam - 1 year, 1 month ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...