Geometric mean in geometry
Large version
of the image
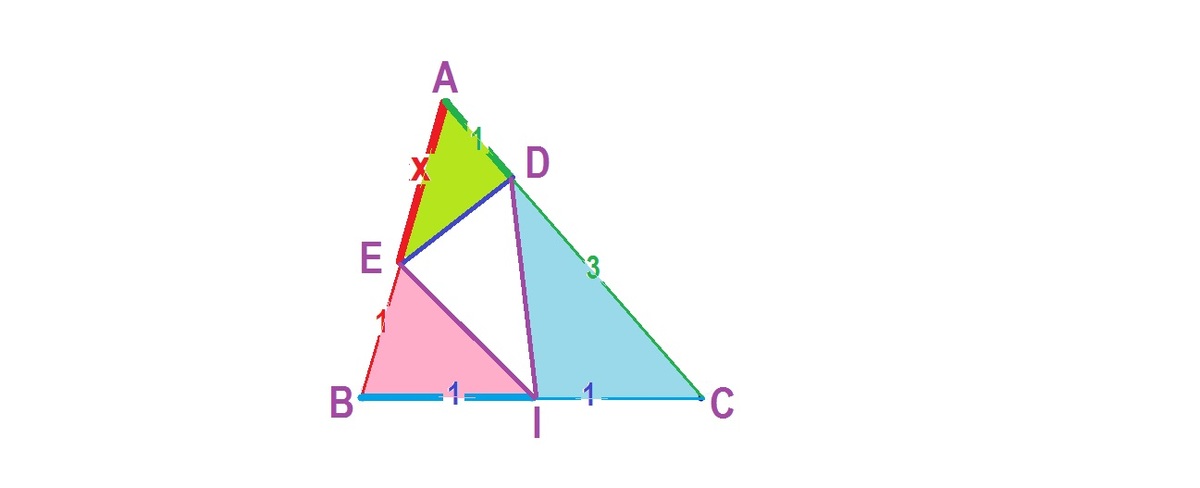
For
△
A
B
C
,
I
is the midpoint of
B
C
, point
D
is in line segment
A
C
such that
C
D
=
3
A
D
and point
E
is in line segment
A
B
such that
[
B
I
E
]
=
[
C
I
D
]
×
[
A
D
E
]
.
If the ratio E B A E can be expressed as c a − b , then find a + b + c .
(The figure is not drawn to scale)
Note: [ X Y Z ] denotes the area of triangle X Y Z .
The answer is 114.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
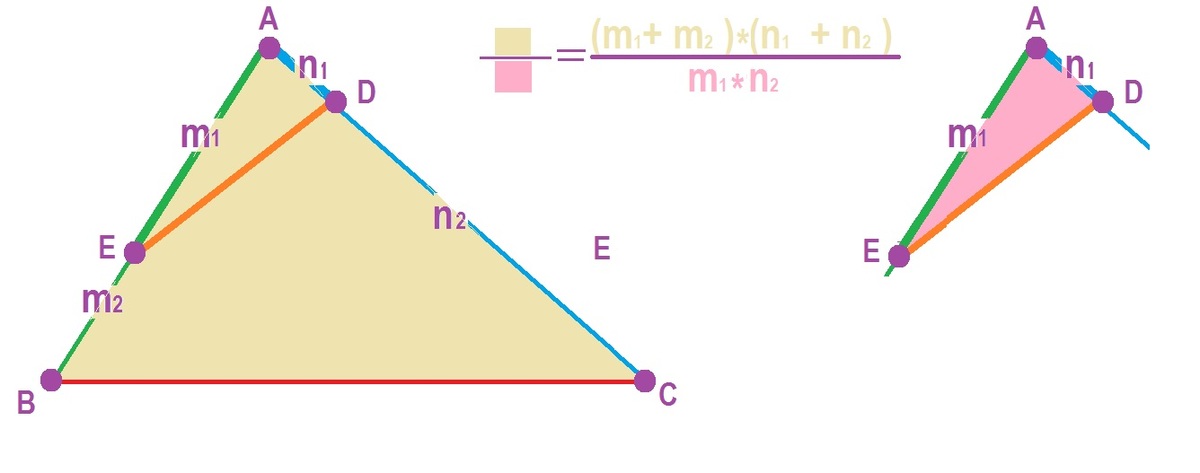L
e
t
A
E
=
X
,
a
n
d
E
B
=
1
L
e
t
a
r
e
a
Δ
A
B
C
=
S
A
B
C
S
B
I
E
=
2
1
∗
1
+
X
1
∗
S
A
B
C
.
S
C
I
D
=
2
1
∗
4
3
∗
S
A
B
C
.
S
A
D
E
=
4
1
∗
1
+
X
X
∗
S
A
B
C
.
∴
(
2
1
∗
1
+
X
1
∗
S
A
B
C
.
)
2
=
(
2
1
∗
4
3
∗
S
A
B
C
.
)
∗
(
4
1
∗
1
+
X
X
∗
S
A
B
C
)
.
⟹
1
+
X
1
=
8
3
∗
X
∴
3
X
2
+
3
X
−
8
=
0
.
S
o
l
v
i
n
g
t
h
e
q
u
a
d
r
a
t
i
c
X
=
6
−
3
+
9
+
9
6
=
6
−
3
+
1
0
5
.
B
u
t
E
B
A
E
=
X
.
∴
a
+
b
+
c
=
1
1
4
.
Same solution . Nice a good presentation .
Same solution.Hats off to your great presentation.