Geometric Motivations

Geometry Level 4

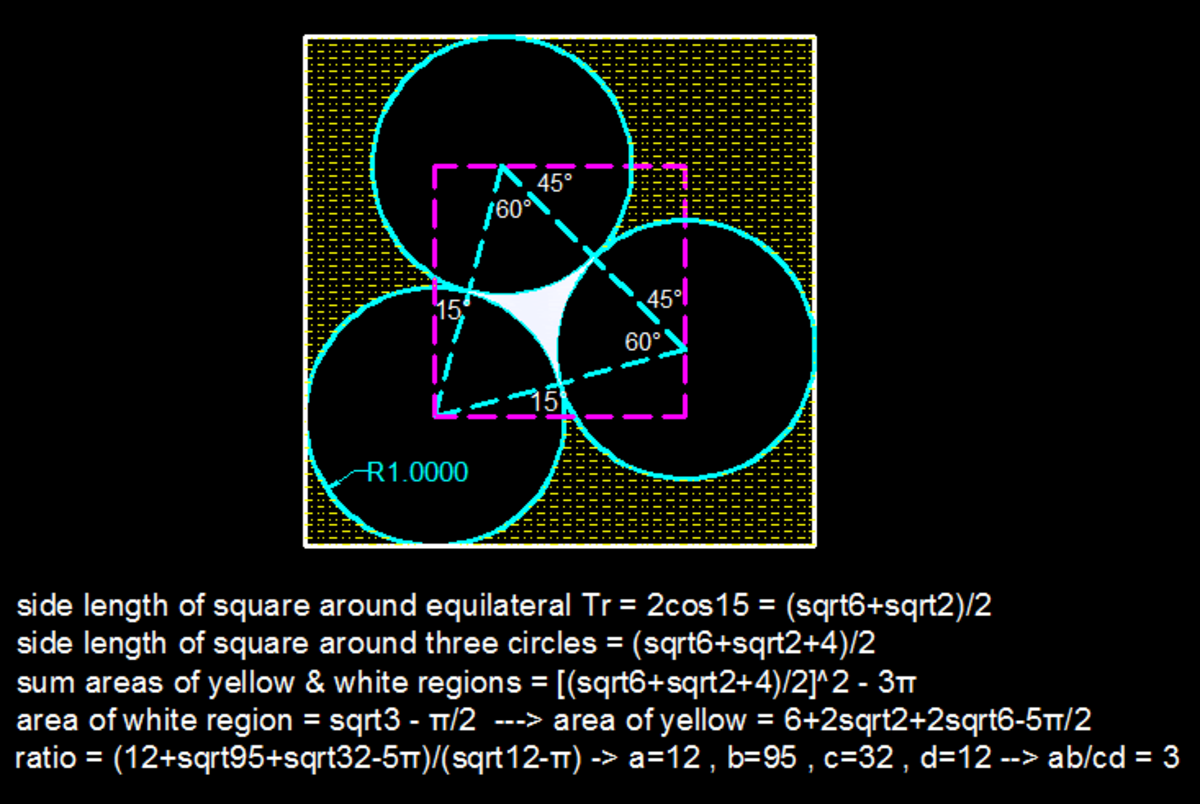
In the figure shown above, 3 unit circles are squeezed into the smallest square possible.

If the ratio of the area of the yellow region to the area of the white region can be expressed as

a + b + c − 5 π d − π , \dfrac{a + \sqrt b + \sqrt c - 5\pi}{\sqrt d - \pi } ,

where a , b , c , d a,b,c,d are all positive integers with b > c b>c , find a b c d \dfrac{ab}{cd} .

Hint: The first step is to find the square side length.


The answer is 3.

Aziz Alasha by Aziz Alasha , 59, Sudan

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions


R i g h t v e r t i c a l s i d e o f t h e s q u a r e = r a d i u s o f O 1 + p r o j e c t i o n o f c e n t e r d i s t a n c e O 1 O 2 , 1 5 o t o v e r t i c a l + r a d i u s o f O 2 . W h i t e a r e a = ( a r e a o f e q u i l a t e r a l t r i a n g l e o f c e n t e r s O 1 O 2 O 3 ) − ( s u m o f a r e a s o f ‘ 3 c o l o r e d s e c t o r s o f t h e 3 c i r c l e s ) T h e R a t i o = g r e e n a r e a w h i t e a r e a = ( a r e a o f t h e s q u a r e ) − ( W h i t e a r e a ) − ( s u m o f a r e a s o f t h e t h r e e c i r c l e s . ) w h i t e a r e a = ( 6 + 2 ∗ 2 + 2 6 + 3 ) − ( 3 − π / 2 ) − ( 3 ∗ π / 2 ) 3 − π / 2 = 12 + 32 + 96 + − π − 6 ∗ π 12 − π = a + c + b − 5 ∗ π d − π ∴ a b c d = 12 ∗ 96 12 ∗ 32 = 3. Right~ vertical~ side~ of~ the~ square~ = ~radius~ of~ O_1~ + ~projection~ of~ center~ distance~~O_1O_2,~~ 15^o~~ to~ vertical~ +~ radius~ of~ O_2.\\ White ~area = (area~ of~ equilateral~ triangle~ of~ centers~ O_1O_2O_3) - (sum ~of ~areas~ of`~ 3 ~colored~ sectors~ of~ the~3~ circles)\\ The~ Ratio=\dfrac{green~area}{white~area}\\ =\dfrac{(area~ of~ the~ square) - (White~ area) - (sum~ of~ areas~of~the~three~circles.) }{white~area} \\ =\dfrac{(6+2*\sqrt2+2\sqrt6+\sqrt3) - (\sqrt3-\pi/2) - (3*\pi/2)}{ \sqrt3-\pi/2}\\ =\dfrac{12+\sqrt{32}+\sqrt{96}+-\pi - 6*\pi}{ \sqrt{12}-\pi}\\ =\dfrac{a+\sqrt{c}+\sqrt{b} - 5*\pi}{ \sqrt{d}-\pi}\\ \therefore~\dfrac{ab}{cd}=\dfrac{12*96}{12*32}=\Large \color{#D61F06}{3}.

0 Helpful 0 Interesting 0 Brilliant 1 Confused
Ahmad Saad
May 23, 2017

b=96 (not 95)

0 Helpful 0 Interesting 0 Brilliant 0 Confused

good morning Mr.Ahmad Saad. please recheck your solution, a=12,b=24,c=8,d=12. therefore ab/cd = 24/8=3. your final answer is correct. thankyou v.much

Aziz Alasha - 4 years ago

Log in to reply

Ratio = [12 + 4sqrt6 + 4sqrt2 - 5π]/[2sqrt3 - π] 

      = [12 + sqrt(6×4^2) + sqrt(2×4^2) - 5π]/[sqrt(3×2^2) - π]

      = [12 + sqrt96 + sqrt32 - 5π]/[sqrt12 - π]

     a = 12  ,  b = 96  ,  c = 32  ,  d = 12

I think that you enter the factors of roots to its roote without squaring it.

Ahmad Saad - 4 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...