Geometric Optics 1
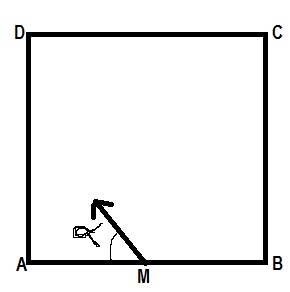 Four identical mirrors
are made to stand vertically to form a square arrangement in the top view.A ray starts from the mid point
of mirror
. After two reflections reaches corner
. Then find
Four identical mirrors
are made to stand vertically to form a square arrangement in the top view.A ray starts from the mid point
of mirror
. After two reflections reaches corner
. Then find
Also see calculus
The answer is 0.75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
There are no complicated calculations involved. In fact, you don't even have to evaluate any trigonometric expressions.
Consider the total horizontal distance traveled. To reach point B , the ray must travel half the square's length, then the entirety of the square's length; this is equal to 2 3 × L .
Now consider the vertical distance traveled. The ray must travel the square's length twice: this is equal to 2 × L .
The cotangent is defined as the quotient of the adjacent leg to the opposite leg, and since we are measuring the angle with respect to the horizontal, cot ( α ) = vertical distance horizontal distance cot ( α ) = 2 L ( 3 / 2 ) L = 4 3