Geometric transformation
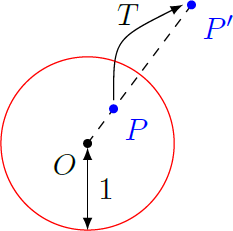
We define for all position vectors in the two-dimensional plane (except the zero vector) a coordinate transformation with Thus, the vectors and point in the same direction, but their lengths are inverse to each other, so that . This transformation is similar to a reflection, since inner part and outer part of the unit circle around are interchanged. This mapping is bijective, so that each point in the plane is uniquely assigned a different point .
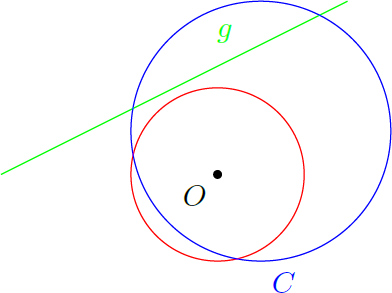
We now consider an arbitrary circle and arbitrary straight line in the two-dimensional plane. We assume that both curves do not go through the origin .
What shape do the curves and take when subjected to the coordinate transformation ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Theorem: T ( C ) and T ( g ) are both circles.
It is easy to exclude that neither C nor g is transformed into a straight line. For each curve γ we can define a distance to the origin by d γ = min P ∈ γ ∣ P ∣ . Since the coordinate transformation inverts the lengths, the point closest to the origin is mapped to a point furthest from the origin. Thus, the image T ( γ ) of curve γ must be within a circle of radius d γ − 1 , because ∣ P ′ ∣ = ∣ P ∣ − 1 ≤ d γ − 1 for each P ∈ γ . Since neither C nor g goes through the origin, their distances are strictly positive ( d C , d g > 0 ), so that their images T ( C ) and T ( g ) are bounded. But a straight line continues to infinity, so that there is a contradiction here.
The proof that the curves are actually circles is much more complicated. In the proof here, which I have worked for myself, I use complex numbers to algebraically represent the transformation. But there may be other proofs that are much shorter or more elegant.
Proof:
We treat the vectors P = ( x , y ) ∈ R 2 as complex numbers z = x + i y = r e i φ ∈ C with real part x = r cos φ and imaginary part y = r sin φ . Thus, the transformation T corresponds to a mapping f : z ↦ z ∗ 1 = r 1 e i φ Therefore, f ( z ) and z have the same phase φ and point in the same direction. Furthermore, ∣ f ( z ) ∣ = r − 1 = ∣ z ∣ − 1 , so that the absolute values are inverse to each other.
A circle around point a with radius R corresponds to the points z = a + ∣ a ∣ a R e i φ = a ( 1 + ρ e i φ ) , ρ = ∣ a ∣ R , φ ∈ [ 0 , 2 π ] We assume ρ = 1 (the origin is not intersected), so that f ( z ) where a ′ R ′ e i φ ′ ∣ e i φ ′ ∣ 2 = a ∗ 1 1 + ρ e − i φ 1 = a ∗ 1 ( 1 − ρ 2 1 − 1 − ρ 2 1 + 1 + ρ e − i φ 1 ) = a ∗ 1 ( 1 − ρ 2 1 − ( 1 − ρ 2 ) ( 1 + ρ e − i φ ) ρ ( ρ + e − i φ ) ) = ( 1 − ρ 2 ) a ∗ 1 ( 1 − ρ 1 + ρ e − i φ ρ + e − i φ ) = a ′ + ∣ a ′ ∣ a ′ R ′ e i φ ′ = ( 1 − ρ 2 ) a ∗ 1 = ∣ a ∣ 2 − R 2 a , = ∣ ( 1 − ρ 2 ) a ∗ ∣ ρ = ∣ ∣ a ∣ 2 − R 2 ∣ R , = − 1 + ρ e − i φ ρ + e − i φ = 1 + ρ e − i φ ρ + e − i φ 1 + ρ e i φ ρ + e i φ = 1 + ρ 2 + 2 ρ cos φ ρ 2 + 1 + 2 ρ cos φ = 1 Therefore φ ′ ∈ R and all points of the image are one a circle with center a ′ and radius R ′ . Since the map f is bijective and continuous, the circle must also be completely traversed.
A straight line that does not go through the origin can be represented in the complex plane by the points z = u + i u λ , λ ∈ R where u is the distance vector from the origin to the line and i u is a direction vector that is parallel to the line. The image of this line then gives f ( z ) where u ′ φ v 2 + w 2 = u ∗ − i u ∗ λ 1 = u ∗ − i u ∗ λ 1 u + i u λ u + i u λ = ∣ u ∣ 2 ( 1 + λ 2 ) u + i u λ = 2 ∣ u ∣ 2 u ( 1 + λ 2 2 + i 1 + λ 2 2 λ ) = 2 ∣ u ∣ 2 u ( 1 − 1 + 1 + λ 2 2 + i 1 + λ 2 2 λ ) = 2 ∣ u ∣ 2 u ( 1 + v 1 + λ 2 1 − λ 2 + i w 1 + λ 2 2 λ ) = u ′ ( 1 + e i φ ) = 2 ∣ u ∣ 2 u , = arctan v w = λ 4 + 2 λ 2 + 1 ( λ 4 − 2 λ 2 + 1 ) + 4 λ 2 = 1 Thus, all points lie on a circle around the point u ′ with the radius ∣ u ′ ∣ . This circle goes in particular through the origin O . However, the origin itself is reached only in the limit case λ → ± ∞ , since lim λ → ± ∞ v = − 1 und lim λ → ± ∞ u = ± 0 . QED
More information about this so-called circle inversion can be found on Wikipedia.