Geometrically invalid
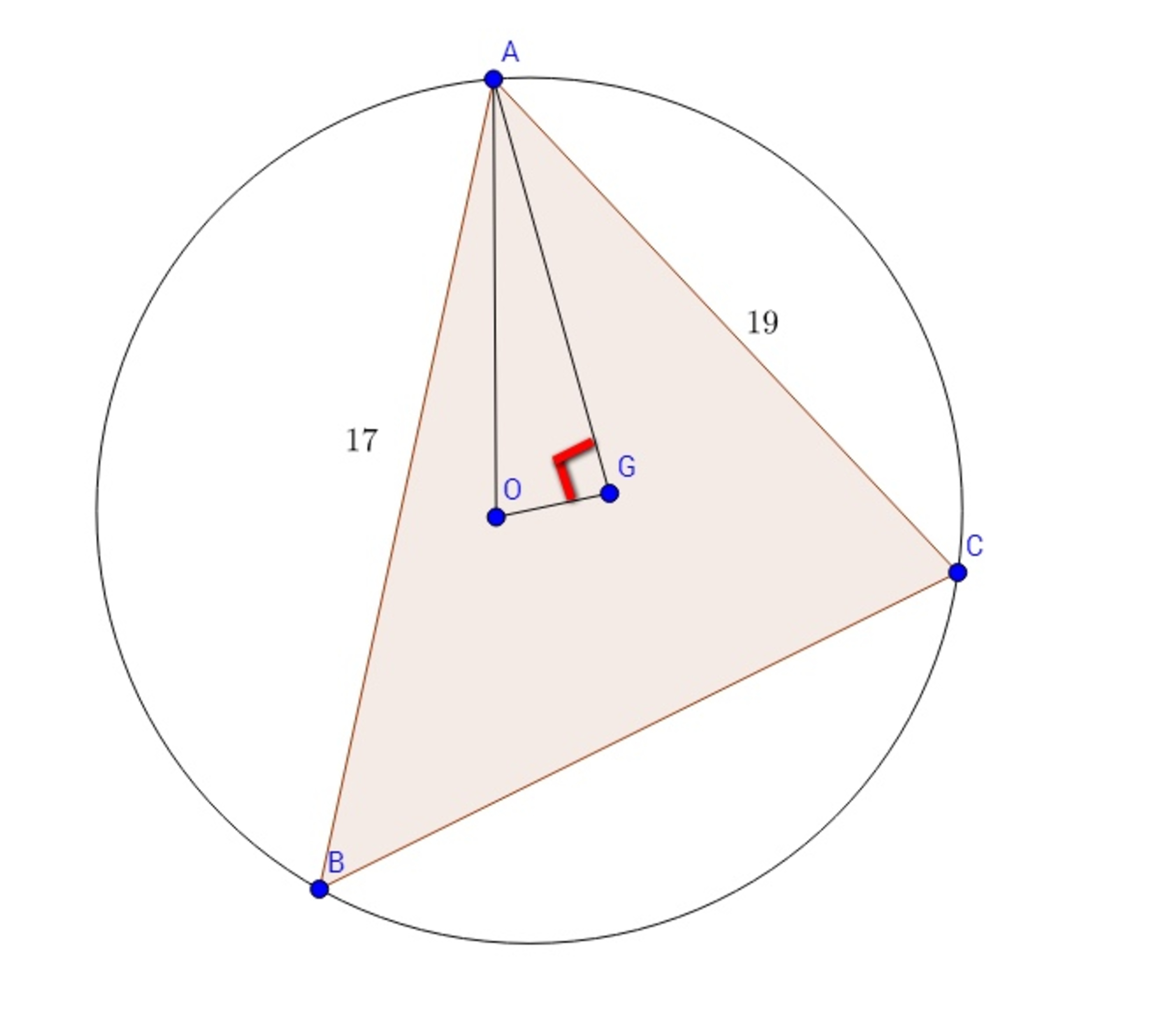
Let and denote the circumcenter and orthocenter of the triangle , respectively. If , find .
Note : Image drawn not necessarily up to scale.
The answer is 325.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If A , B , C have position vectors a , b , c with respect to the circumcentre O as origin (so that a , b , c all have the same modulus R , the circumradius), then the position vectors of G and M (the midpoint of B C are g = 3 1 ( a + b + c ) m = 2 1 ( b + c ) and we require that g ⋅ ( a − m ) = 0 . Thus 0 = = = ( a + b + c ) ⋅ ( 2 a − b − c ) = 2 ∣ a ∣ 2 + a ⋅ ( b + c ) − ∣ b + c ∣ 2 a ⋅ b + a ⋅ c − 2 b ⋅ c 2 1 [ 2 R 2 − A B 2 ] + 2 1 [ 2 R 2 − A C 2 ] − [ 2 R 2 − B C 2 ] and hence B C 2 = 2 1 ( A B 2 + A C 2 ) . In our case, we deduce that B C 2 = 3 2 5 .