Geometrically Perfect Triangle

Using Cosine Rule, we have:

$\overline {BC}^2 = \overline {AB}^2 + \overline {AC}^2 - 2 (\overline {AB}) ( \overline {AC}) \cos {\theta}$

$\Rightarrow \sin^2 {\theta} = 2 \sin {\theta} - 2 \sin {\theta} \cos {\theta} \quad \Rightarrow \sin {\theta} = 2 - 2 \cos {\theta}$

Squaring both sides, we have:

$\sin^2 {\theta} = 4 - 8 \cos {\theta} + 4 \cos^2 {\theta} \quad \Rightarrow 1 - \cos^2 {\theta} = 4 - 8 \cos {\theta} + 4 \cos^2 {\theta}$

$\Rightarrow 5 \cos^2 {\theta} - 8 \cos {\theta} + 3 \quad \Rightarrow ( 5 \cos {\theta} - 3) ( \cos {\theta} -1) = 0$

$\Rightarrow \cos {\theta} = \frac {3}{5}$ , since $\theta \ne 0$ and hence $\cos {\theta} \ne 1$ .

Since $\cos {\theta} = \frac {3}{5}\quad \Rightarrow \sin {\theta} = \frac {4}{5}$ , as $\cos {\theta}$ and $\sin {\theta}$ as 3, 4 and 5 are Pythagorean triplets.

The area of $\triangle ABC$ is given by:

$A = \dfrac {1}{2} \sin {\theta} \sqrt{\sin {\theta}}\cos {\frac {\theta} {2}} = \dfrac {1} {2} \times \dfrac {4}{5} \times \sqrt{\frac {4}{5}} \times \sqrt{\frac {\cos {\theta}-1} {2}}$

$\quad = \dfrac {1} {2} \times \dfrac {4}{5} \times \sqrt{\frac {4}{5}} \times \sqrt{\frac {\frac {3}{5}-1} {2}} = \dfrac {1} {2} \times \dfrac {4}{5} \times \sqrt{\frac {4}{5}} \times \sqrt{\frac {4} {5}} = \dfrac {8}{25} = \dfrac {m}{n}$

$\Rightarrow m + n = 8 + 25 = \boxed {33}$

In triangle ABC,

we have, BC=a= root (sin theta) AB=AC=b=c= sin (theta)

now we know that, cos(A)= (b^2+ c^2- a^2)/ 2bc as angle A= theta we have,

    cos (theta) = 2sin(theta) - sin(theta)^2 / 2 sin(theta)

==> 2 sin (theta) cos (theta) = 2sin(theta) - sin(theta)^2 ==> sin(theta)^2 = 2 sin (theta) { 1 - cos(theta) } ==> sin(theta)^2 = 2 sin (theta) 2 sin(theta/2)^2 from further calculation we get,

tan (theta) =4/3 so sin(theta) =4/5.

now the area of triange ABC= 1/2. b. c. sin(A) = 1/2 sin(theta)^2 = 1/2 . 16/25 = 8/25

so, m+n =8+25 =33

I would be really grateful if anyone edited by comment in LATEX :)

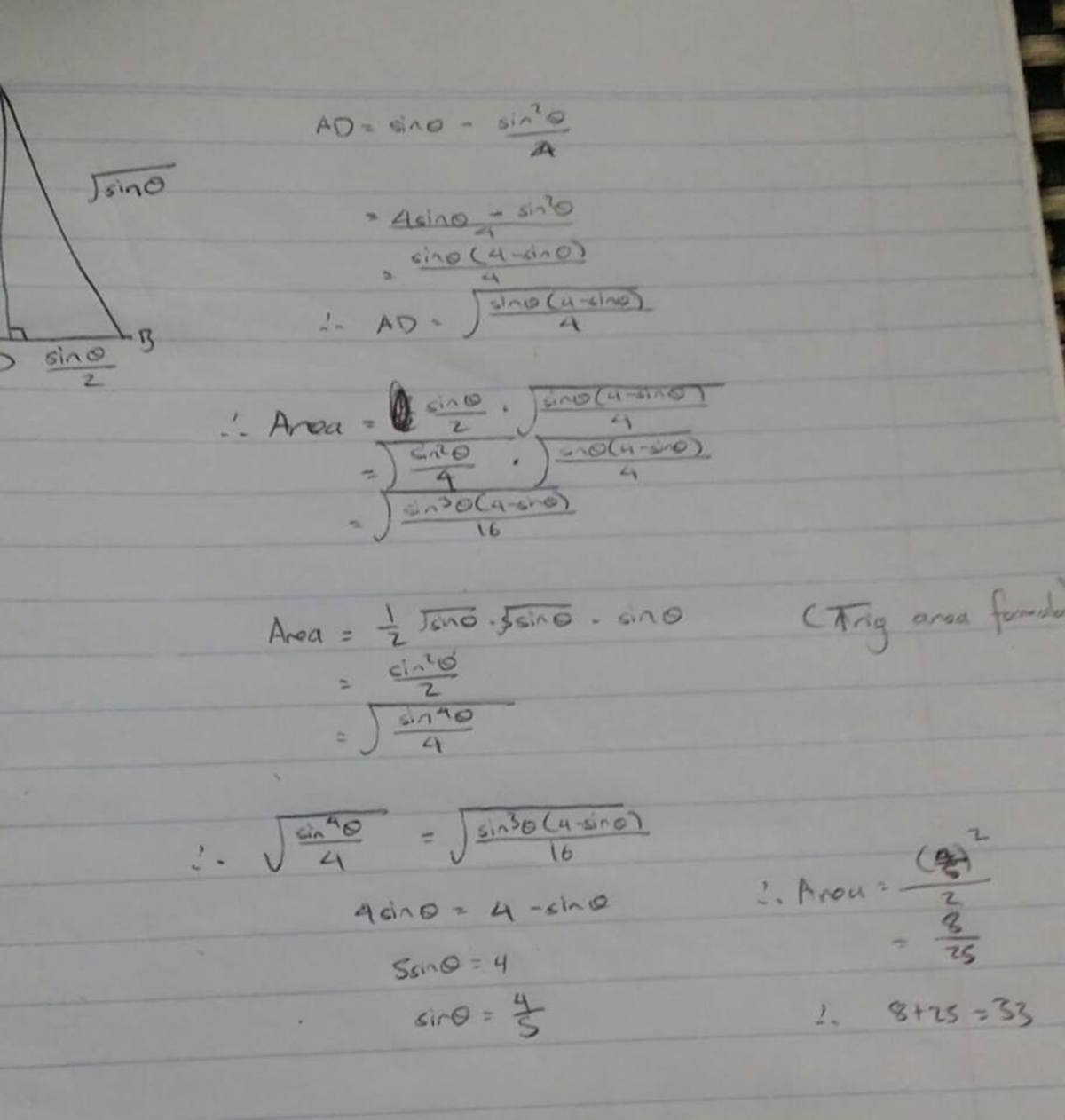
Why use trig when u can use algebra : ) Btw, that number that u can barely read just above the answer is (4/5).

First, we have that $\angle B = \angle C = \frac{\pi}{2} - \frac{\theta}{2}$ .

Next, using the Sine Law, we have that

$\frac{\sin(\angle B)}{\sqrt{\sin(\theta)}} = \frac{\sin(\theta)}{\sin(\theta)} \Longrightarrow \sin(\angle B) = \sqrt{\sin(\theta)} \Longrightarrow \cos(\frac{\theta}{2}) = \sqrt{\sin(\theta)}$ .

Now square both sides and use the identity $\cos(\theta) = 2\cos^{2}(\frac{\theta}{2}) - 1$ to find that

$\cos(\theta) + 1 = 2\sin(\theta)$ .

Square both sides again and use the identity $\sin^{2}(\theta) + \cos^{2}(\theta) = 1$ to find that

$5\cos^{2}(\theta) + 2\cos(\theta) - 3 = 0 \Longrightarrow (5\cos(\theta) - 3)(\cos(\theta) + 1) = 0$ .

The only valid solution in this case is thus $\cos(\theta) = \frac{3}{5}$ , which in turn gives us that $\sin(\theta) = \frac{4}{5}$ .

$\Delta ABC$ thus has side lengths $\frac{4}{5}, \frac{2\sqrt{5}}{5}, \frac{2\sqrt{5}}{5}$ . A quick application of Heron's formula yields an area value of $\frac{8}{25}$ .

Thus $m = 8, n = 25$ and $m + n = \boxed{33}$ .