Geometricum geometriorum (HP IV, Goblet of fire)
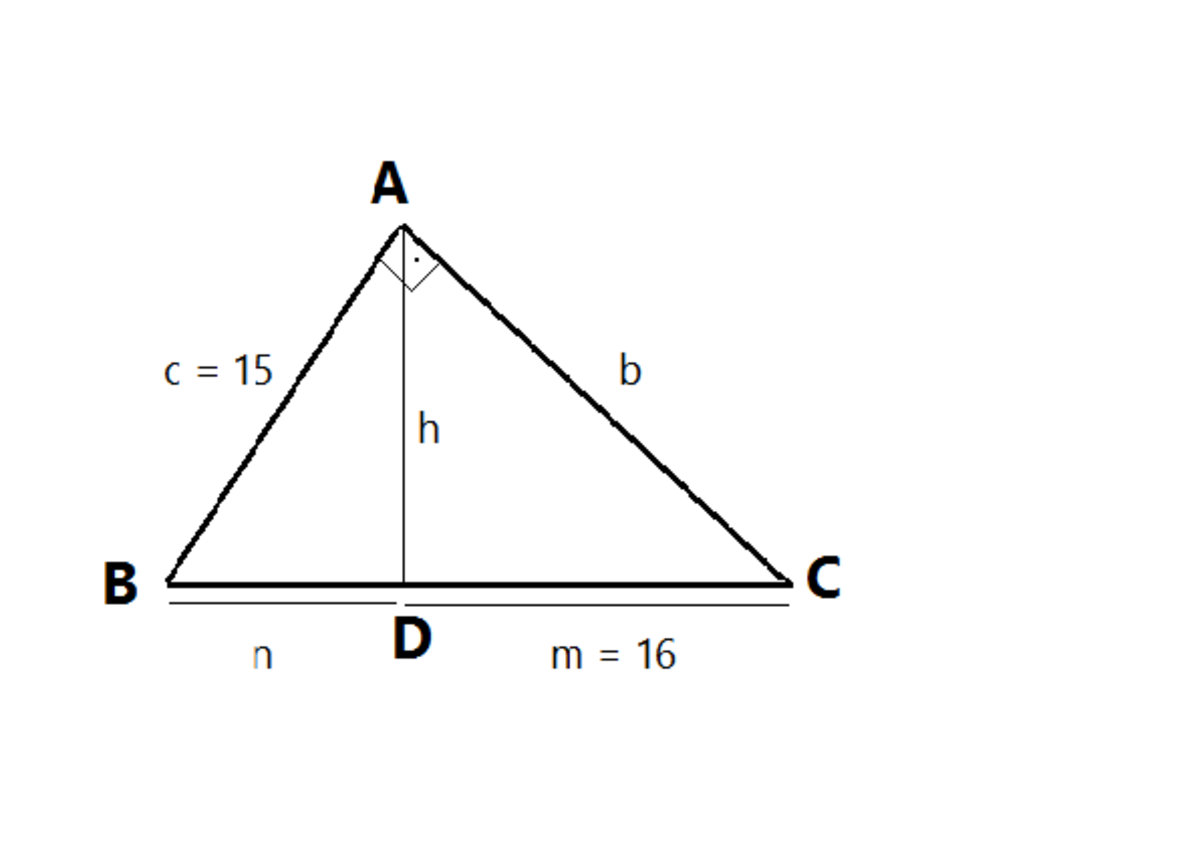
The right- triangle shown above, ( ), has , and . Find the altitude (height) from to with foot at , the lenght of side and .
Submit
The answer is 41.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
∠ A B C = x ⟹ ∠ A C B = 9 0 − x In Δ A B D ∠ B A D = 9 0 − x = ∠ A C B In Δ A C D ∠ C A D = x = ∠ A B C In Δ A B C and Δ D B A ∠ B A C = ∠ A D B = 9 0 ∠ B A D = ∠ A C B ⟹ Δ A B C Δ D B A (AA) ⟹ B D A B = A B B C ⟹ A B 2 = B C ⋅ A B ⟹ 1 5 2 = n ( n + 1 6 ) ⟹ 2 2 5 = n ( n + 1 6 ) ⟹ n = 9 , − 2 5 ⟹ n = 9 In Δ A B C B C 2 = A B 2 + A C 2 ⟹ b = A C 2 = B C 2 − A B 2 = 4 0 0 ⟹ b = 2 0 In Δ A D B Δ A B C Δ D B A ⟹ D B A B = A D A C ⟹ 9 1 5 = h 2 0 ⟹ h = 1 2 ∴ n + b + h = 1 2 + 2 0 + 9 = 4 1