Geometry #1
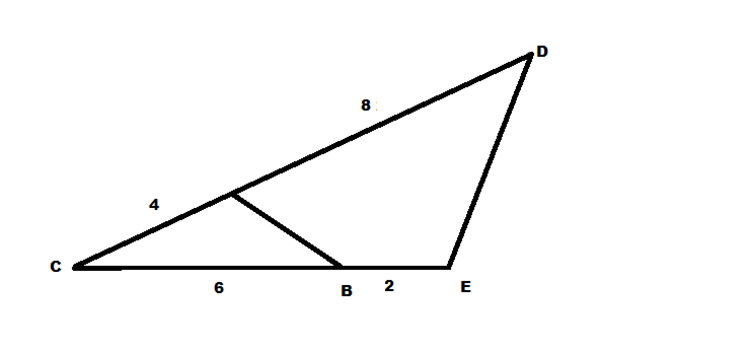 If the area of Δ ABC is 3 square units, and the lengths are given on the figure, then find the area of Δ CDE
If the area of Δ ABC is 3 square units, and the lengths are given on the figure, then find the area of Δ CDE
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The area of △ A B C is 3, and the base is 6. So, we can get the equation for area 2 6 h = 3 . Solving for h , we get h = 1 . Now, C D is just segment C A , but 3 times. It has the exact same slope the whole time. That means that if we were to extend segment C E to 8 units long, while retaining its slope and position of point C , then the height from the new point e to the base would be 2. Since it is 3 ∗ C A , the height of △ C D E is 3. The base, obviously, is 8, and we get a = 2 8 ∗ 3 = 2 2 4 = 1 2 . So 12 is the answer!
For this question, we can use the formula {1/2 ab sin c} to calculate the area of a triangle, where c is an arbitrary angle. So we know that [ABC] =3. Using the above formula, we can find the arbitrary angle c to be roughly 14.478 deg. As the arbitrary angle for triangles CDE and ABC are same, then employ the same formula so the answer would be 1/2 x (4+8) x (3+2) x sin 14.478 which is 12.0004... Which is rounded to 12. ! Do note that this method may have some rounding off errors and adjustments so please use this method when you have to employ this equation for only a few times for accuracy and precision.