Geometry

Consider the diagram above.

$\dfrac{a}{b+8}=\dfrac{5}{10}$ $\color{#D61F06}(1)$

$\dfrac{b}{a+5}=\dfrac{8}{10}$ $\color{#D61F06}(2)$

From $\color{#D61F06}(1)$ ,

$a=\dfrac{5b+40}{10}$ $\color{#D61F06}(3)$

Substitute $\color{#D61F06}(3)$ in $\color{#D61F06}(2)$ , we have

$\dfrac{b}{\dfrac{5b+40}{10}+5}=\dfrac{8}{10}$

$\dfrac{b}{\dfrac{5b+40+50}{10}}=\dfrac{8}{10}$

$\dfrac{b}{1}\left(\dfrac{10}{5b+90}\right)=\dfrac{8}{10}$

$\dfrac{10b}{5b+90}=\dfrac{8}{10}$

$100b=40b+720$

$60b=720$

$b=12$

It follows that,

$a=\dfrac{5(12)+40}{10}=\dfrac{100}{10}=10$

Finally,

$a+b=10+12=$ $\boxed{22}$

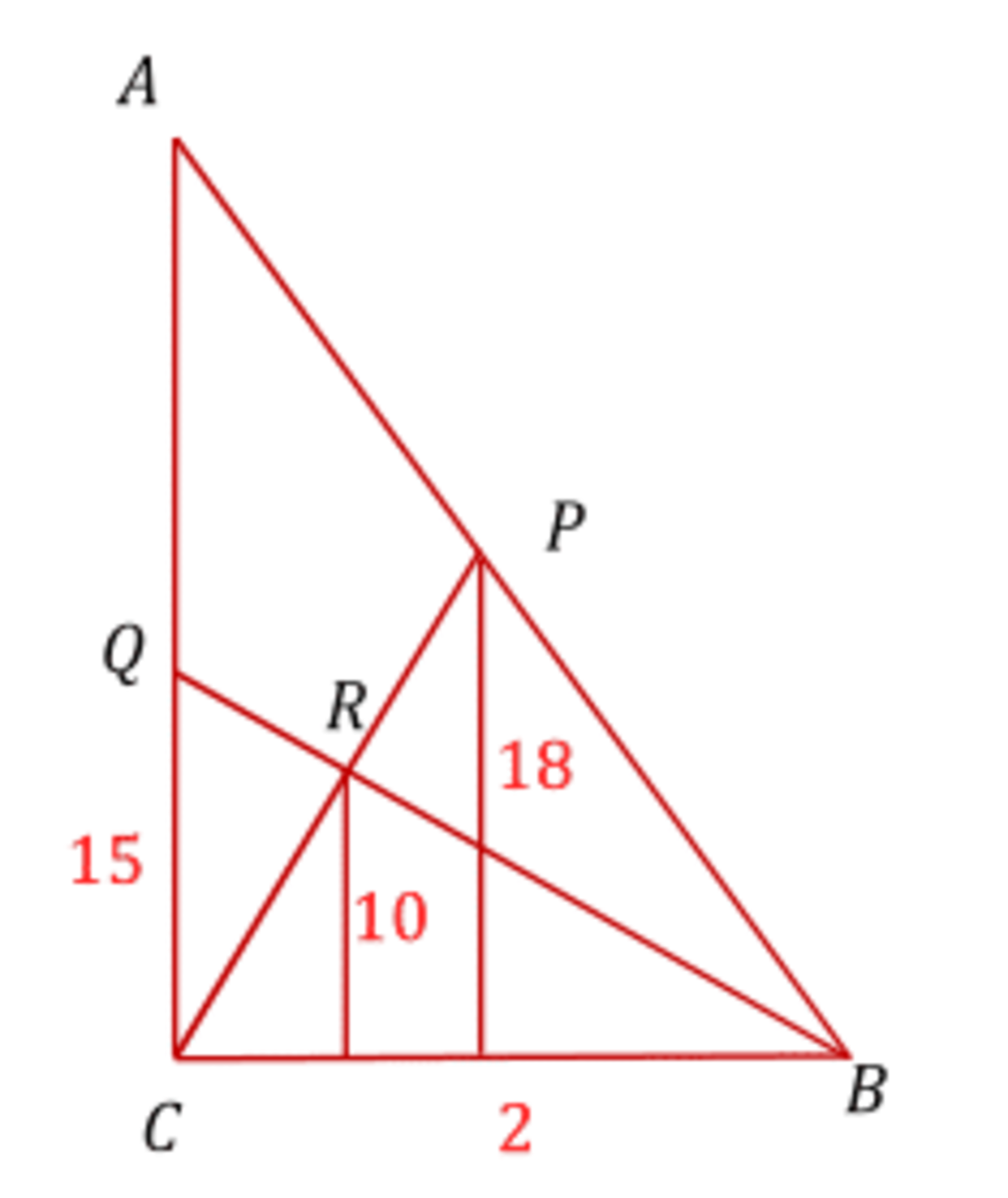The areas of triangles are as follows: $[CBR]=10, [CBQ]=10+5=15, [CBP]=10+8=18$

Since the breakdown into base and height is not given, we can use whatever is convenient. I have chosen to make the common base $2$ , so that the heights of the triangles are simply equal to their areas.

Likewise it does not matter where the heights are located, so I have chosen $\angle ACB=90^\circ$ and placed the origin of my coordinate system at $C$

Equation of the line through $QB$ is $y=15-\dfrac{15}{2}x$

Point $R$ is located on this line at $y=10$ , so the coordinates of the point are $R=\left(\dfrac23, 10\right)$

Line $CP$ goes through point $R$ and has the form $y=kx$ . It is therefore given by equation $y=15x$

The point $P$ is located on this line where $y=18$ and has coordinates $P=\left(\dfrac65, 18\right)$

Line $AB$ has the format $y=b-\dfrac b2 x$ and goes through point $P$ , so it is $y=45-\dfrac{45}{2}x$

The $y$ -intercept of this line is $b=45$ so the area of the triangle $ABC$ is $[ABC]=45$

The area of the quadrilateral $[AQRP]=45-10-5-8=\boxed{22}$