Geometry
Geometry
Level
pending
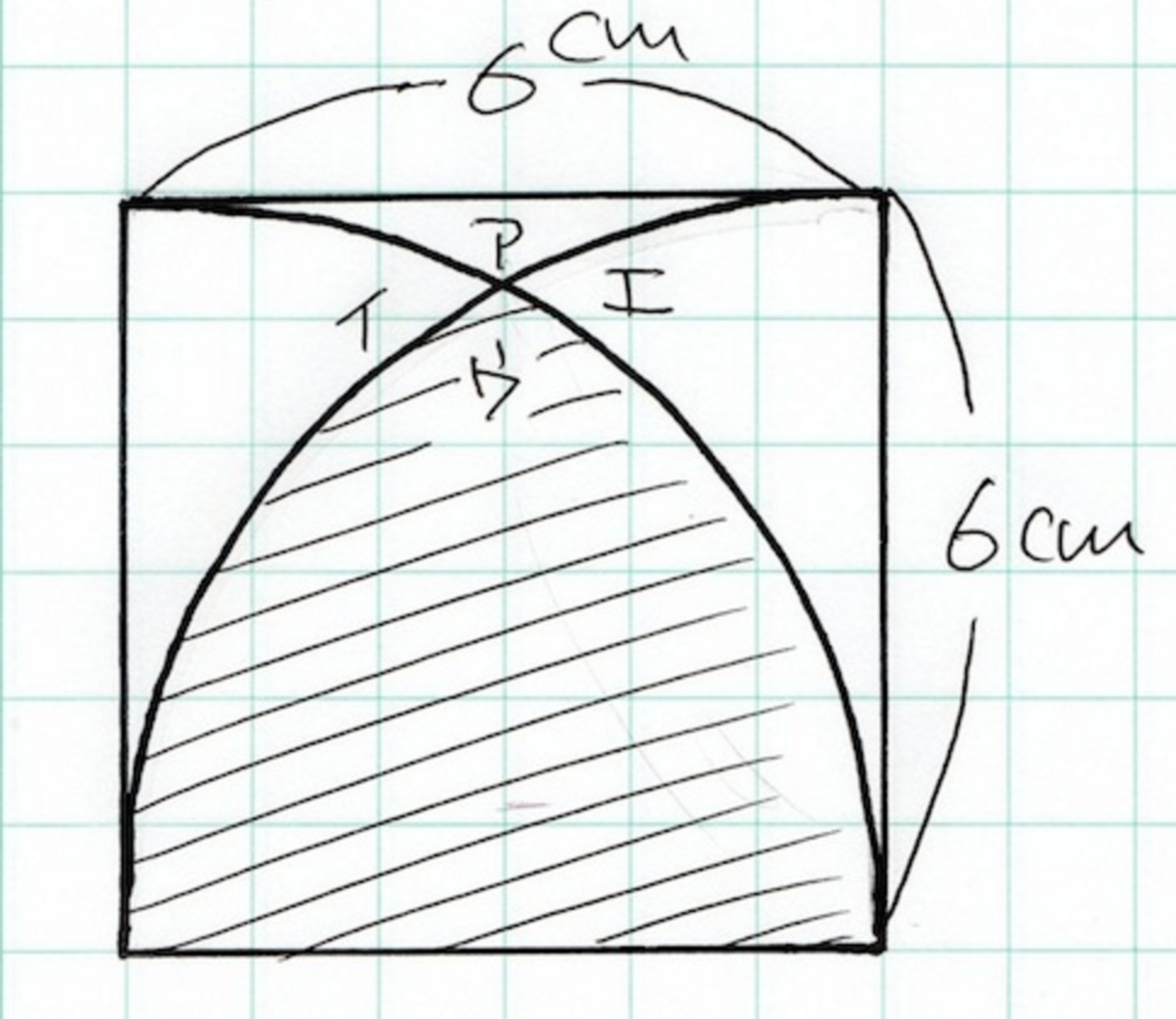
What is the approximate total area of the shaded area?
22.48
31.4
15.7
62.8
20.36
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, draw an equilateral triangle inside the shaded area. One side should be 6cm in length
There should also be two semi-circular shapes outside the triangle.
The area of the triangle - (using the Pythagoras theorem, we know that the height of the triangle is sqrt of 26)
3 6 sqrt(26)/2 = 3*sqrt(26)
The area of two semi-circular shapes - 6 * 6 * 3.14 * 60/360
18.84*2=37.78
37.78 - 3*sqrt(26) =22.482941