Geometry?
Find the minimum value of
x 2 + ( 2 0 − y ) 2 + y 2 + ( 2 1 − z ) 2 + z 2 + ( 2 0 − w ) 2 + w 2 + ( 2 1 − x ) 2 .
The answer is 58.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
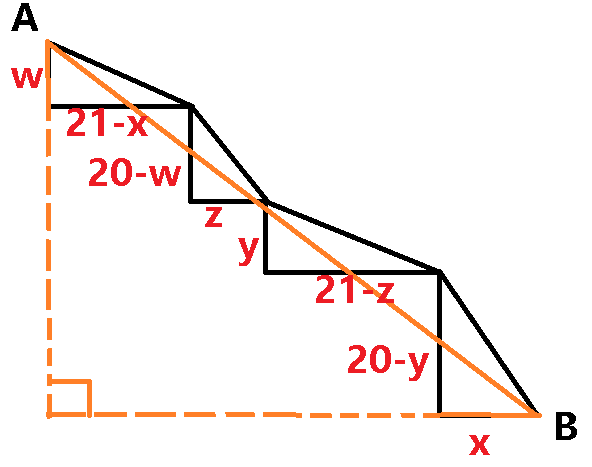Minimum value is the length of
A
B
, that is
4
2
2
+
4
0
2
=
5
8
what will be x,y,z,w when it is 58?
how does someone even think of something like this..?
Why not interchange X and w. That way we get 2*41^2. Plz explain
Differentiating the function partially w.r.t. each variable and equating to 0, we get the value of the variables as,
X
=
Z
=
2
2
1
,
W
=
Y
=
1
0
.
Substituting these values in the expression,
w
e
g
e
t
(
2
2
1
)
2
+
1
0
0
+
1
0
0
+
(
2
2
1
)
2
+
(
2
2
1
)
2
+
1
0
0
+
1
0
0
+
(
2
2
1
)
2
=
4
∗
(
1
0
0
+
(
2
2
1
)
2
=
5
8
Why have you taken w= 10 ? , to get min. value we should take w=20 and thus we get 54 as minimum value all other variable has same value as suggested by you. if i am wrong please correct me