Geometry
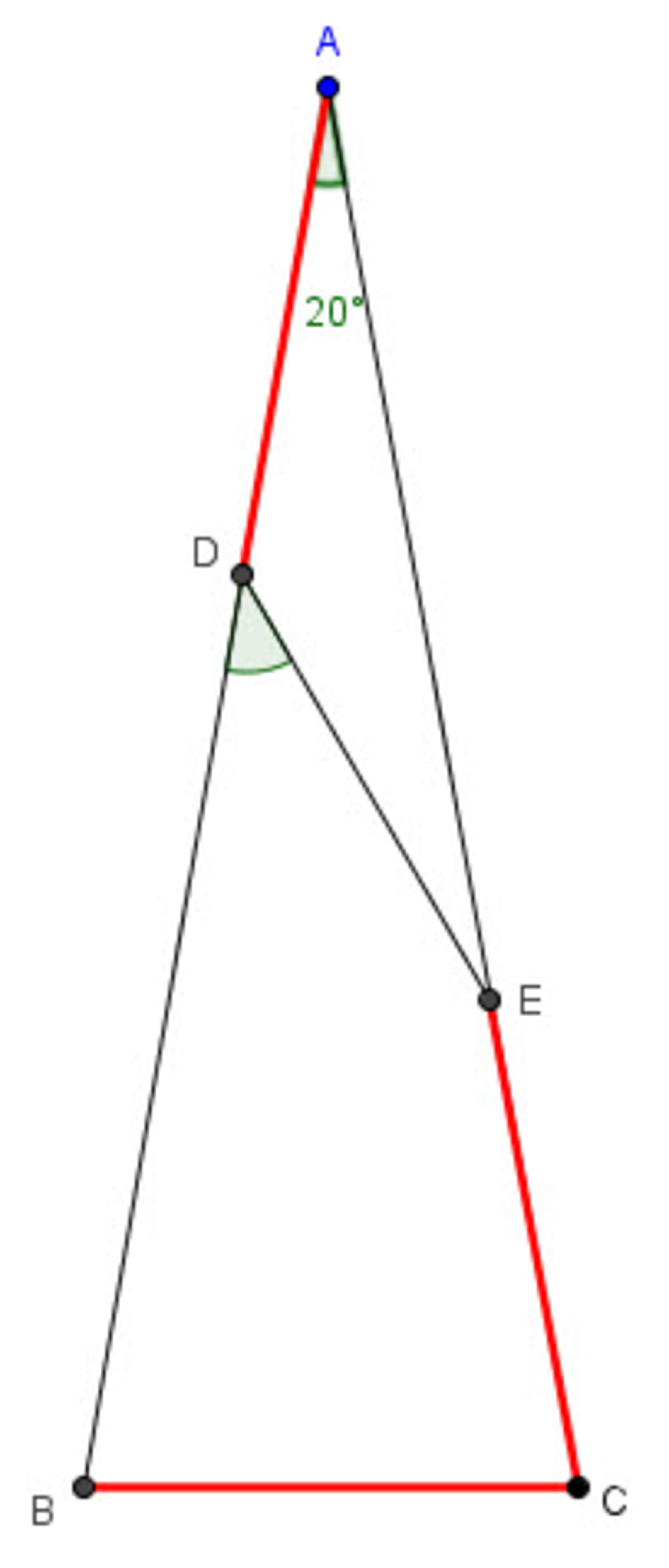
In the isosceles triangle ABC, , . Find the measure of angle in degrees.
The answer is 40.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
In parallelogram F E G C this will give us G C = F E = 2 1 .
From △ A B G the full side A B = 2 sin 1 0 ∘ 1 = 2 . 8 7 9 and the section of it in the middle D H = 2 . 8 7 9 − 2 = 0 . 8 7 9
Projection of this section into the vertical D F = 0 . 8 7 9 × cos 1 0 ∘ = 0 . 8 6 6
From right △ D F E the ∠ F D E = arctan D F E F = 3 0 ∘
To get desired angle, we add the ∠ F D H = 1 0 ∘ and get 3 0 ∘ + 1 0 ∘ = 4 0 ∘ .
The really interesting result is obtained when we calculate the length of D E = cos 3 0 ∘ 0 . 8 6 6 = 1 .
A line made of four equal segments attached by flexible joints will fold perfectly into a narrow isosceles triangle with the top angle of 2 0 ∘ .