Geometry
A regular five star is inscribed in a circle of radius 10

If A denote the area of shaded region
Find 8 . 8 4 1 A
The answer is 992.464.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Sorry for that , can you change the answer. upvoted
Log in to reply
I have updated the answer to 992.464
@megh choksi You should clarify what a "regular five star" is. It is not immediately obvious that the 2 edges lie on the same line.
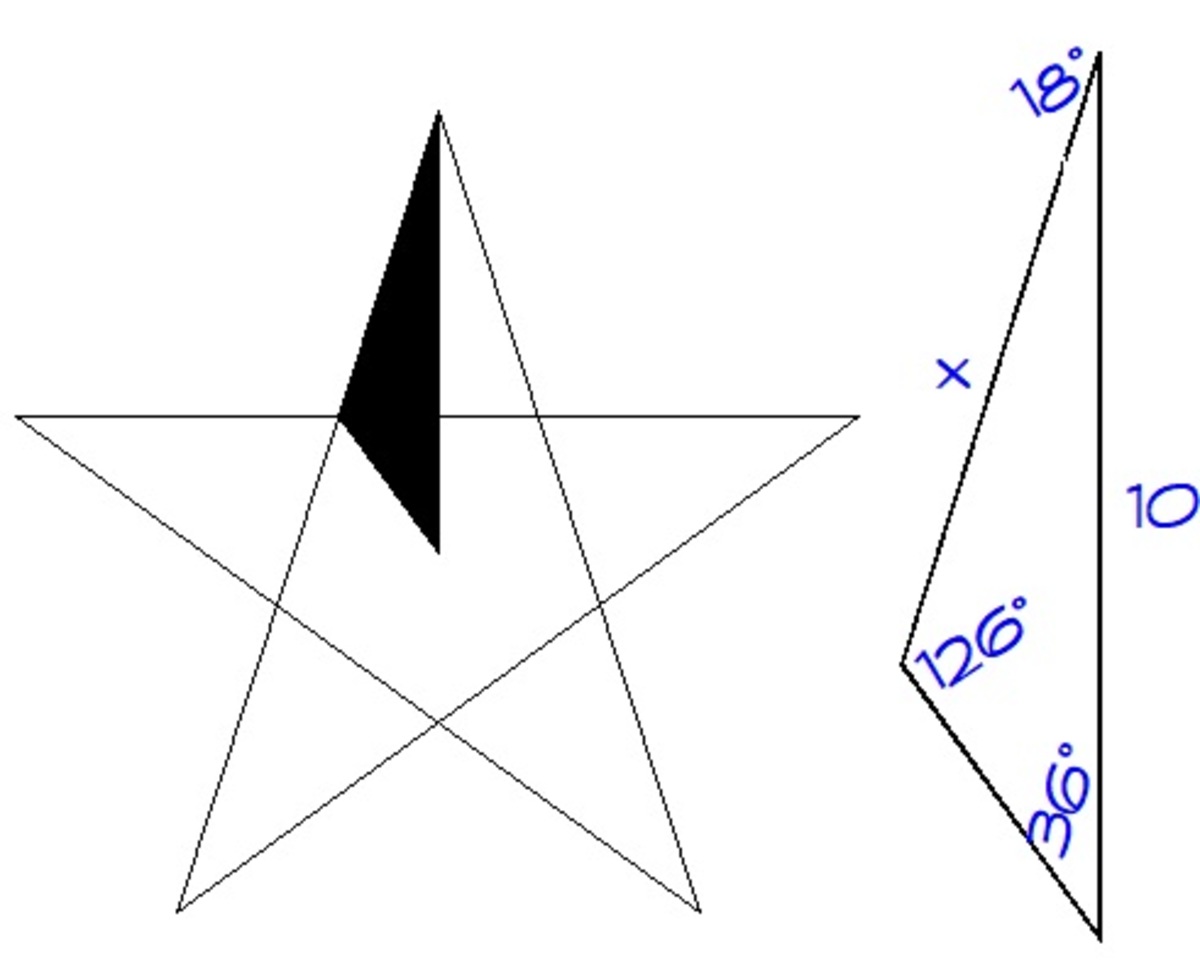
By sine law, we have
sin 3 6 x = sin 1 2 6 1 0
x ≈ 7 . 2 6 5 4
A = 1 0 ( 2 1 ) ( x ) ( 1 0 ) ( sin 1 8 ) = 5 ( 7 . 2 6 5 4 ) ( 1 0 ) ( sin 1 8 ) ≈ 1 1 2 . 2 5 7
The desired answer is 8 . 8 4 1 ( 1 1 2 . 2 5 7 ) = 9 9 2 . 4 6 4
Let A be the top vertex of the star, O be the center of the star, (and circle), and B be the vertex of the star immediately below and to the right of A . Thus A O = 1 0 .
Since the interior angle of each of the 'points' of the star is one-half the central angle of a pentagon, we have that ∠ O A B = ( 2 1 ) ( 2 1 ) 7 2 ∘ = 1 8 ∘ .
Now the star is composed of 1 0 triangles congruent to Δ A O B , and thus ∠ A O B = ( 1 0 1 ) 3 6 0 ∘ = 3 6 ∘ .
This means that ∠ A B O = 1 2 6 ∘ . Now use the Sine Law on Δ A O B to find that A B = A O ∗ sin ( 1 2 6 ∘ ) sin ( 3 6 ∘ ) = 1 0 ∗ tan ( 3 6 ∘ ) .
Thus Δ A O B has a base length of 1 0 and a height of 1 0 ∗ tan ( 3 6 ∘ ) sin ( 1 8 ∘ ) , and so the area of the star is
A = 1 0 ∗ ( 2 1 ) ∗ 1 0 ∗ 1 0 ∗ tan ( 3 6 ∘ ) sin ( 1 8 ∘ ) = 5 0 0 ∗ tan ( 3 6 ∘ ) sin ( 1 8 ∘ ) .
The solution is then 8 . 8 4 1 ∗ A = 9 9 2 . 4 6 4 to 3 decimal places.
(This differs slightly from the posted answer of 9 9 2 . 5 2 4 , (probably due to rounding), so I'm guessing that any answer that rounds to 9 9 2 . 5 will be considered correct.)