Geometry Again!
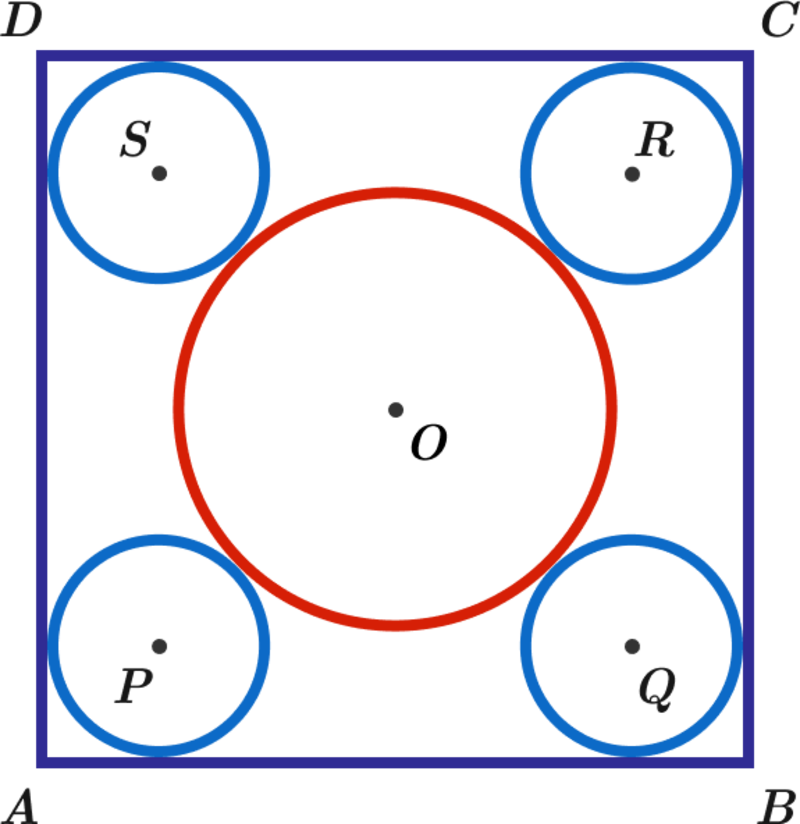
In the adjoining diagram, is a square. The larger circle has center which is also the center of the square. The smaller circles have equal radii and are each tangent to the square and the larger circle. The area of the larger circle is equal to the sum of the areas of the smaller four circles. What is the ratio between the side length of the square and the radius of a smaller circle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
So the distance O R = 3 r .
The line O R is a part of the diagonal and at 4 5 ∘ angle with the vertical, so its projection into the vertical, E R = 3 r c o s ( 4 5 ∘ ) = 2 3 r .
Add to this the distance R T = r and we’ll have half the side of the square, a .
Therefore a = 2 ( 2 3 r + r ) = r ( 2 + 3 2 ) and the ration r a = 2 + 3 2 .