Geometry and Calculus of Binweed Flowers

There is a little calculus trick to get a quite accurate answer:

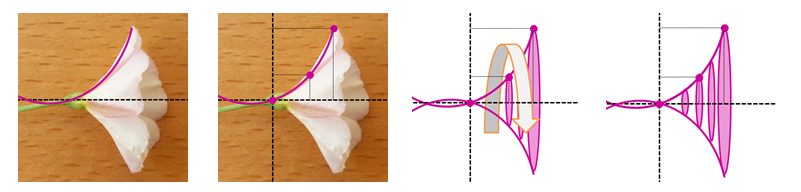
Splitting the flower in the middle, we recognize, that the curved side forms part of a square function.

If we draw three points (x-axis = height; y-axis = diameter): $(0|0)$ for the flower knot, which we set in the origin of the coordinate system, $(0.75|0.5)$ for the radius $\frac{1}{2}*1$ at half the height $\frac{1}{2}*1.5$ and $(1.5|1.25)$ for half the diameter at the top, we can arrange the following linear system (three times substitution of the square formula: $y(x) = a*x^2 + b*x + c$ :

• I.: $0 = a*0^2 + b*0 + c$

• II.: $0.5 = a*0.75^2 + 0.75*0 + c$

• III.: $1.25 = a*1.5^2 + 1.5*0 + c$

And solving for $a, b, c$ and substituting the general formula, we get $y(x) = 0.222*x^2 + 0.5*x + 0$ .

Imagine rotating this function around the x-axis. It will form the same body our flower encloses. To get this volume, we multiply the integral of the $y(x)^2$ with $\Pi$ . That is a really cool calculus-formula! To understand it better: Imagine that calculating the square for every $y(x)$ within the integral range with $\pi$ equals calculating the area of a slice at $x$ . And as an integral gives us the sum of the values, we mathematically "stack" those slices back on top of each other and get the volume.

Here in formulas:

$\pi * \int_{1.5}^{0} (0.222*x^2 + 0.5*x)^2 dx$

$\pi * \int_{1.5}^{0} (0.049284*x^4 + 0.222*x^3 + 0.25*x^2) dx$

and as we only have to calculate for the upper limit (as everything times and minus 0 stays the same) we get:

$\pi * (\frac{0.049284*x^5}{5}+\frac{0.222*x^4}{4}+\frac{0.25*x^3}{3})$

$\pi * (\frac{0.049284*1.5^5}{5}+\frac{0.222*1.5^4}{4}+\frac{0.25*1.5^3}{3})$

$= 2.001 cm^3$

Here as visual process to follow along (without end-volume as I haven't found a fitting visualization):