Geometry fraction
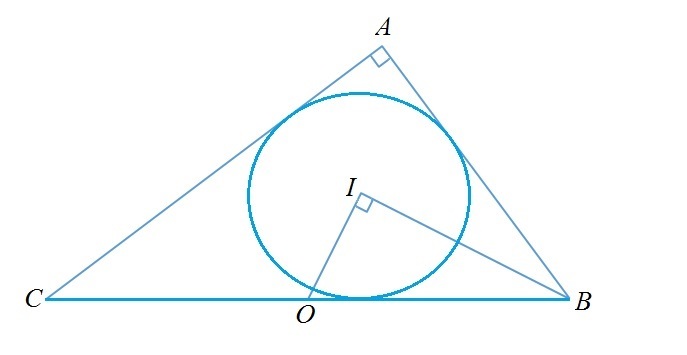 In the triangle
A
B
C
,
∠
B
A
C
=
9
0
o
and
A
C
>
A
B
.
O
is the midpoint of
B
C
and
I
is the center of incircle of a triangle
A
B
C
. If
∠
B
I
O
=
9
0
o
, what is the value of
A
C
A
B
?
In the triangle
A
B
C
,
∠
B
A
C
=
9
0
o
and
A
C
>
A
B
.
O
is the midpoint of
B
C
and
I
is the center of incircle of a triangle
A
B
C
. If
∠
B
I
O
=
9
0
o
, what is the value of
A
C
A
B
?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Can we go pure geometric? That will be a bit smarter .
Log in to reply
Wait and see if there are other solutions. Guess I am not that smart.
I attempted to solve it using trigonometry but resorted to geometry.
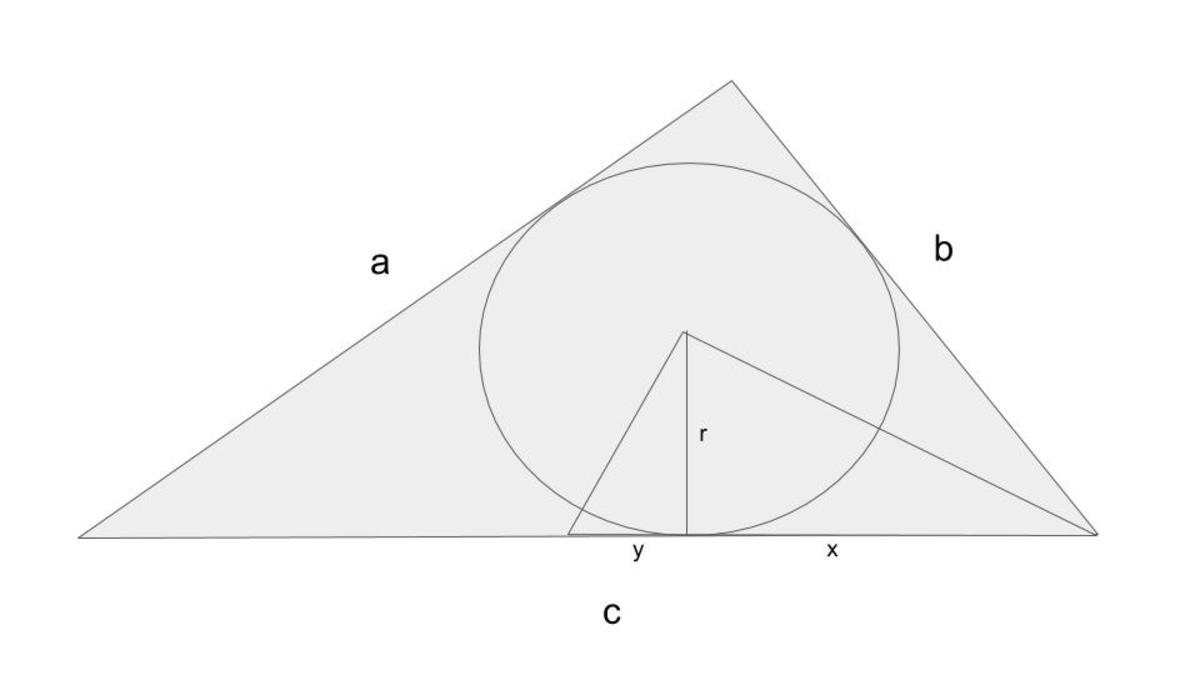 c
=
2
(
x
+
y
)
- given
c
=
2
(
x
+
y
)
- given
a = c − x + r - inspection
b = x + r - inspection
r y = x r implies r = x y
Therefore
a = x + 2 y + x y
b = x + x y
Since c 2 = a 2 + b 2 we can solve for y in terms of x , obtaining (after a lot of algebra) y = 4 x , so that a b = 4 3 .
I am curious if anyone else did it this simple way, if they found an elegant way to do the algebra. Mine was ugly.
Let B C be a and the altitude of △ B I C and △ B I O , I D = h . We note that:
△ B I O : tan θ h + tan ( 9 0 ∘ − θ ) h tan θ h + cot θ h tan θ 1 + tan θ = O B = 2 a = 2 h a . . . ( 1 )
△ B I C : tan θ h + tan ( 4 5 ∘ − θ ) h tan θ h + 1 − tan θ h ( 1 + tan θ ) tan θ 1 + 1 − tan θ 1 + tan θ = B C = a = h a . . . ( 2 )
2 ( 1 ) = ( 2 ) : tan θ 2 + 2 tan θ tan θ 1 + 2 tan θ ( 1 − tan θ ) ( 1 + 2 tan 2 θ ) 1 − tan θ + 2 tan 2 θ − 2 tan 3 θ 2 tan 3 θ − tan 2 θ + 2 tan θ − 1 ⟹ tan θ = tan θ 1 + 1 − tan θ 1 + tan θ = 1 − tan θ 1 + tan θ = tan θ ( 1 + tan θ ) = tan θ + tan 2 θ = 0 = 2 1
Now we have A C A B = tan 2 θ 1 = 2 tan θ 1 − tan 2 θ = 2 × 2 1 1 − 4 1 = 4 3