It's an integer right?
The sides of a △ A B C are the tangents to the parabola y 2 = 4 a x . Let D , E , F be the points of contact of side B C , C A and A B respectively. If lines A D , B E , C F are concurrent at the focus of the parabola.
Let the ∠ A B C be α π . Find the value of α α − 8 .
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
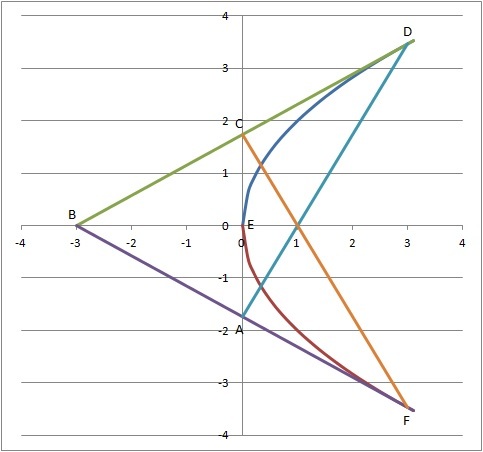
△ A B C with sides tangential to the parabola y 2 = 4 a x has to be an isosceles triangle as shown above. A C is along the y-axis and B on the x-axis.
Let y D of D ( x D , y D ) be b , then x D = 4 a b 2 ⇒ D ( 4 a b 2 , b ) .
The gradient of the parabola is given by:
2 y d x d y = 4 a ⇒ d x d y = y 2 a
At point D , gradient is m = b 2 a .
Therefore, for point B , we note that:
x D − x B b = m = b 2 a
⇒ x B = x D − 2 a b 2 = 4 a b 2 − 2 a b 2 = − 4 a b 2 = − x D
We note that point C is mid-point of D B and therefore, C ( 0 , 2 b ) and A ( 0 , − 2 b ) .
Considering the line A D passing throught the focus ( a , 0 ) , we have:
2 b a = b 4 a b 2 − a ⇒ 2 a = 4 a b 2 − a ⇒ b 2 = 1 2 a 2 ⇒ b = 2 3 a
Let ∠ A B C = θ , then tan 2 θ = 2 a b 2 b = b 2 a = 2 3 a 2 a = 3 1
⇒ ∠ A B C = θ = 2 tan − 1 ( 3 1 ) = 2 × 6 π = 3 π
⇒ α = 3 ⇒ α α − 8 = 1 9 .
You are missing a 2 in the denominator is the line where you have tan(theta/2) = 2a/b = (2a)/(a 2 sqrt(3)*a)
Log in to reply
Thanks, I have corrected it and corrected another error.
Consider a symmetric case. So T1T2 meet axis perpendicularly at M. Tangents meet at B on the axis. And tangent AC perpendicular to axis at vertex O.
Property of parabola: MO = OB.
Thus T2M = 2 OC = 2 OA.
Hence AT2 intersects OM in ratio 1:2, giving FM = 2 OF = 2a.
This gives x coordinate of T1, T2 as 3a. So the y coordinates of T1, T2 will be + 1 2 a and − 1 2 a
Slope of tangent to y 2 = 4 a x will be y ′ = y 2 a = 1 2 a 2 a = 3 1
Hence inclination of tangent BA = 30 degrees! Giving the desired angle to be 60 degrees. And the triangle ABC to be an equilateral triangle.
Angle = 6 0 ° = π / 3 giving α = 3 Hence α α − 8 = 3 3 − 8 = 2 7 − 8 = 1 9