Geometry is Awesome!
Chords A B and P Q meet at K and are perpendicular to one another. If A K = 4 , K B = 6 and P K = 2 , find the area of the circle.
Submit your answer to the nearest integer .
The answer is 157.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
how do you know that the distance from point m to the center is 1 ?
Log in to reply
Sorry, I did not adequately describe it. The perpendicular ON from center O to chord AB much bisect it. So AN = 5 of which AK is given to be 4. So NK must be 1.
-
- Daigram is not to scale
- As shown above AB CD are perpendicular and 'h' and 'i' are perpendiculars to the chords
- We know AH=4,HB=6,HC=2
- And we know
- A H × H B = C H × H D
- thus , HD=12
- Now AG = 5,ED=7
- AG-AH=GH
- GH=5-4
- GH=1=EF (since EFGH is a rectangle)
- Now in right angled triangle EDF
- F E 2 + E D 2 = F D 2
- Thus F D = F E 2 + E D 2 = 7 2 + 1 2 = 5 0
- AREA = π r 2 =3.14 x 50= 1 5 7
perfect solution...+1
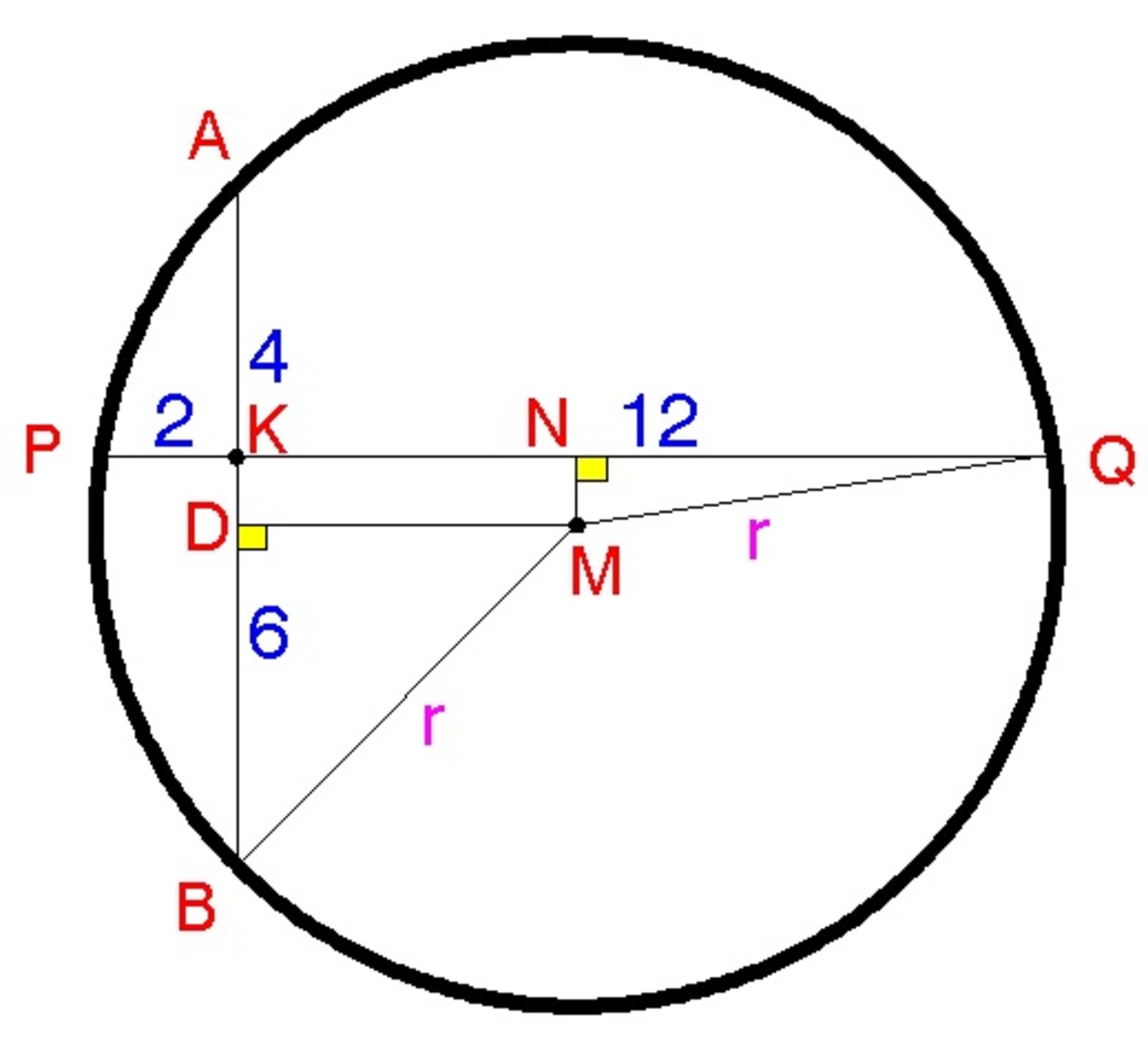
Solving for K Q , we have
( K Q ) ( 2 ) = ( 4 ) ( 6 ) ⟹ K Q = 1 2
Draw perpendiculars form M to K Q or K B ,
N Q = 2 2 + 1 2 = 7
D B = 2 4 + 6 = 5
N M = D K = 6 − 5 = 1
D M = K N = 7 − 2 = 5
By Pythagorean Theorem, we have
r 2 = 1 2 + 7 2 = 5 0 or r 2 = 5 2 + 5 2 = 5 0
Solving for the area of the circle, we have
A = π r 2 = π ( 5 0 ) 2 = 1 5 7
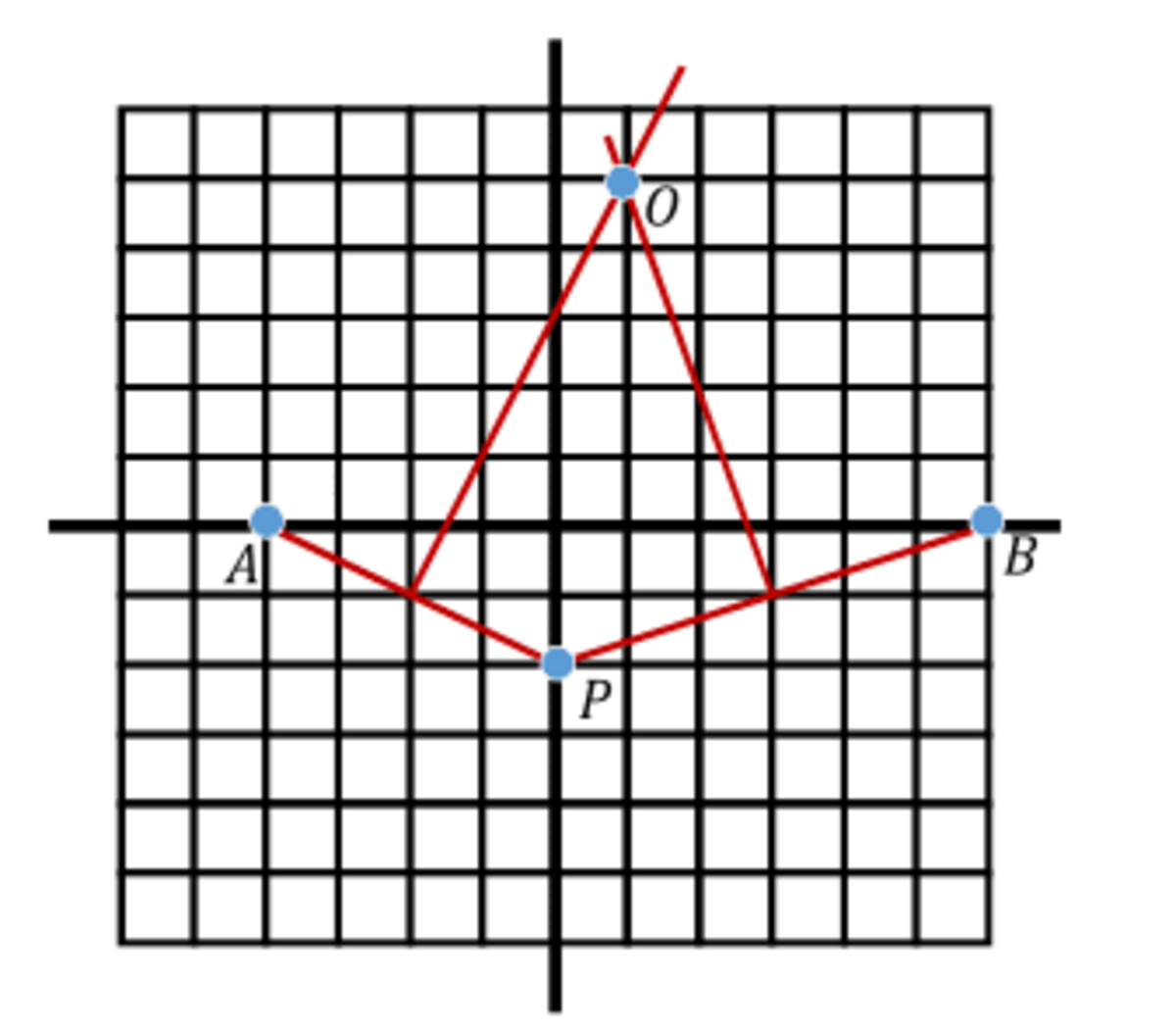 Calculation can be almost completely replaced by sketching when numbers are this easy. Put the points in the grid as shown above. Connect them. Run perpendicular lines, making sure the slopes are correct. Find where they intersect (point
O
in the sketch). Points
A
and
O
are off by
5
both in
x
and
y
directions, so the distance between them is
R
=
5
2
, giving us the area as
π
×
5
2
×
2
≈
1
5
7
.
Calculation can be almost completely replaced by sketching when numbers are this easy. Put the points in the grid as shown above. Connect them. Run perpendicular lines, making sure the slopes are correct. Find where they intersect (point
O
in the sketch). Points
A
and
O
are off by
5
both in
x
and
y
directions, so the distance between them is
R
=
5
2
, giving us the area as
π
×
5
2
×
2
≈
1
5
7
.
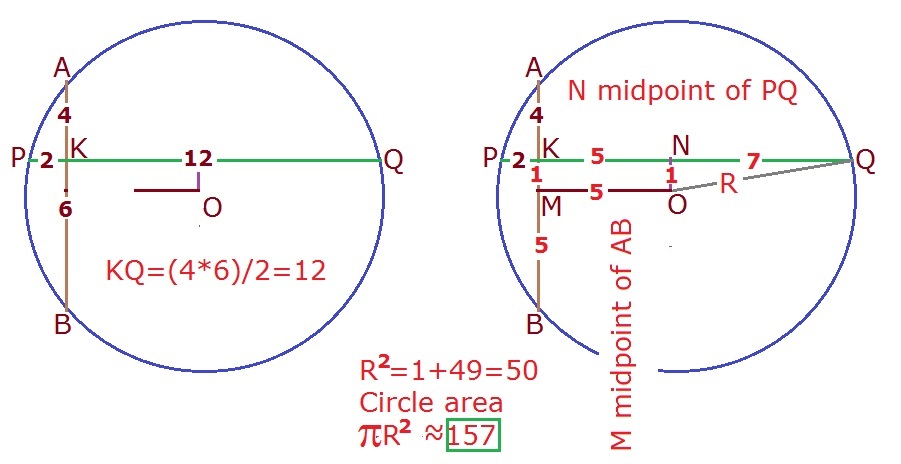
Let perpendiculars ON and OM to the chords, form a rectangle KNOM. NK = MO = 1, NB = 5
R 2 = O P 2 = ( h + 2 ) 2 + 1 2 and
R 2 = O B 2 = h 2 + 5 2 Solving gives h = 5 and R 2 = 5 0 giving area = 1 5 7