Geometry is not that bad
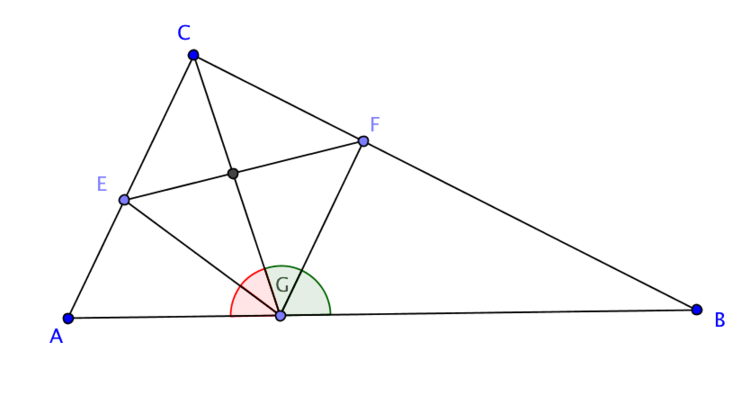 In a triangle
△
A
B
C
we draw a cevian through C that touches AB at G. The angle bisector of
△
B
G
C
touches BC at F and the angle bisector of
△
C
G
A
touches CA at E. If you know
F
G
= 33 and
G
E
= 56. What is
E
F
?
In a triangle
△
A
B
C
we draw a cevian through C that touches AB at G. The angle bisector of
△
B
G
C
touches BC at F and the angle bisector of
△
C
G
A
touches CA at E. If you know
F
G
= 33 and
G
E
= 56. What is
E
F
?
The answer is 65.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Some people are not in your level Michael, you should explain it in order that everybody can understand!
∠ E G F = 9 0 ∘ because ∠ B G F + ∠ F G C + ∠ C G E + ∠ E G A = 1 8 0 ∘ and because ∠ B F G = ∠ F G C = α and ∠ C G E = ∠ E G A = β we have 2 α + 2 β = 1 8 0 ∘ ⟹ α + β = 9 0 ∘ and from here Michael Ng solution follows.
By the way, I didn't want to sound rude, thanks Michael for bothering writing a solution!!
thanx dude :D
<AGC +<BGC=180° So the sum of the angles formed by angle bisector is 90°. Right angle! Cheers! Pythagoras theorem...
<EGF is 90. Then using Pythagorean theorem, EF = sqrt(33 33 + 56 56) = 65
Notice that ∠ E G F = 9 0 ∘ so by Pythagoras' Theorem E F = 6 5 .