Geometry Meets Computer Science

Computer Science Level 4

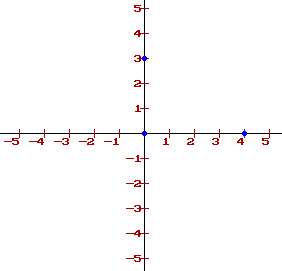Example 1 : Suppose you have a string of 6 integers such as: 000340

These digits represent the three co-ordinates on the Cartesian plane $(0,0),(0,3)$ and $(4,0)$ .

If lines are drawn to connect each of the points, you form a triangle. Your task is to calculate the area of this triangle (given its co-ordinates). Clearly the above triangle has an area of 6 units squared.

Example 2 :

Suppose you have a string of 6 integers such as: 556739

These digits represent three co-ordinates on the Cartesian plane $(5,5), (6,7), (3,9)$ .

If lines are drawn to connect each of these points, you form a triangle. After doing the calculations, the area of the above triangle has an area of 4 units squared.

You are provided with a text file containing the co-ordinates for each triangle.

Find the triangle with the largest area. Report the value for the area to one decimal place

Details and Assumptions

Each string in the text file will always contain 6 non-negative integers and the $x$ and $y$ value of each co-ordinate will always be a integer between 0 and 9. In other words, the given co-ordinates will always be in the first quadrant.

The answer is 23.5.

7 solutions

Ww Margera
Aug 20, 2015

Bash one-liner:

awk '{a=int($1/100000);b=int($1/10000)%10;c=int($1/1000)%10;d=int($1/100)%10;e=int($1/10)%10;f=$1%10;i=c-a;j=d-b;k=e-a;l=f-b;p=((i\*l)-(j\*k));if (p<0){p=-p};print $1,p/2}' o1|sort -rg -k 2,2|head -n 1

781381 23.5

Great to see good old unix one liners

Agnishom Chattopadhyay - 5 years, 9 months ago

Oussama Boussif
Aug 3, 2015

Just use shoelace formula, the rest is easy: $A\quad =\quad \frac { 1 }{ 2 } \left| \left( { x }_{ a }-{ x }_{ c } \right) \left( { y }_{ b }-{ y }_{ a } \right) -\left( { x }_{ a }-{ x }_{ b } \right) \left( { y }_{ c }-{ y }_{ a } \right) \right|$

Beakal Tiliksew
Aug 2, 2015

A rough solution in python

from math import sqrt
import string

def dis(a,b,c,d):
    return sqrt((a-c)**2+(d-b)**2)

def area(n):
   a,b,c,d,e,f=int(n[0]),int(n[1]),int(n[2]),int(n[3]),int(n[4]),int(n[5])
   A= dis(a,b,c,d)
   B= dis(a,b,e,f)
   C= dis(c,d,e,f)

   s = (A + B + C) / 2
   area = (s*(s-A)*(s-B)*(s-C)) ** 0.5 #heron's formula
   return area

largest=0

with open("file.txt", "r") as num:
    for line in num:
      if line.strip():
         largest=max(largest,area(line))


print largest

Serena Chan
Mar 25, 2016

My Java solution below. Not the most elegant but may be easier to understand.

package main;

import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;

public class TrianglePoints {

    public static class Cood {
        private int x, y;

        public Cood(int x, int y) {
            this.x = x;
            this.y = y;
        }

        public int getX() {
            return x;
        }

        public int getY() {
            return y;
        }
    }

    public static class Triangle {
        private Cood a, b, c;

        public Triangle(Cood a, Cood b, Cood c) {
            this.a = a;
            this.b = b;
            this.c = c;
        }

        private double calcAB() {
            return calcLength(a, b);
        }

        private double calcBC() {
            return calcLength(b, c);
        }

        private double calcAC() {
            return calcLength(a, c);
        }

        private static double calcLength(Cood a, Cood b) {
            return Math.sqrt(Math.pow(a.getX() - b.getX(), 2) + Math.pow(a.getY() - b.getY(), 2));
        }

        public double calcArea() {
            return calcArea(calcAB(), calcBC(), calcAC());
        }

        private static double calcArea(double a, double b, double c) {
            double s = (a + b + c) / 2;
            return Math.sqrt(s * (s - a) * (s - b) * (s - c));
        }
    }

    public static void main(String[] args) {
        double maxA = 0;
        BufferedReader br = null;
        try {
            br = new BufferedReader(new FileReader(new File("/Users/justausername/anotherfile/TrianglePoints.txt")));
            String line = br.readLine();
            while (line != null) {
                Triangle t = new Triangle(new Cood(line.charAt(0), line.charAt(1)),
                        new Cood(line.charAt(2), line.charAt(3)), new Cood(line.charAt(4), line.charAt(5)));
                double cA = t.calcArea();
                if (maxA < cA) {
                    maxA = cA;
                }
                line = br.readLine();
            }
        } catch (Exception e) {
            e.printStackTrace();
        }

        finally {
            if (br != null) {
                try {
                    br.close();
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            System.out.printf("%.1f", maxA);
        }
    }

}

Hey Serena! To a fellow JAVA coder, this is a great object-oriented programming approach to this problem.

Mark Mottian - 5 years, 2 months ago

Bill Bell
Jan 8, 2016

from math import sqrt

class Triangle:
    def __init__(self,Ax,Ay,Bx,By,Cx,Cy):
        self.__Ax=Ax
        self.__Ay=Ay
        self.__Bx=Bx
        self.__By=By
        self.__Cx=Cx
        self.__Cy=Cy
    def __distance(self,x1,y1,x2,y2):
        return sqrt((x1-x2)**2+(y1-y2)**2)
    def sides(self):
        return ( self.__distance(self.__Ax,self.__Ay,self.__Bx,self.__By),
            self.__distance(self.__Bx,self.__By,self.__Cx,self.__Cy),
            self.__distance(self.__Cx,self.__Cy,self.__Ax,self.__Ay) )
    def __Heron(self,a,b,c):
        s=(a+b+c)/2.
        return sqrt(s*(s-a)*(s-b)*(s-c))
    def area(self):
        return self.__Heron(*self.sides())

maxArea=0
for line in file('triangles.dat').readlines():
    Ax,Ay,Bx,By,Cx,Cy=map(float,list(line[:-1]))
    maxArea=max(Triangle(Ax,Ay,Bx,By,Cx,Cy).area(),maxArea)
print maxArea

Abdelhamid Saadi
Aug 2, 2015

This is a solution in python 3.4:

def det(p1, p2, p3):
    return detv((p2[0] - p1[0], p2[1] - p1[1]), (p3[0] - p2[0], p3[1] - p2[1]))

def detv (v1, v2):
    return v1[0]*v2[1] - v2[0]*v1[1]


def surface(stri):
    lst = [int(d) for d in stri]
    return abs(det((lst[0],lst[1]), (lst[2],lst[3]), (lst[4],lst[5])))/2

def solve():
    "Geometry Meets Computer Science"
    f = open("TrianglePoints.txt")
    triangles = f.read().split("\n")
    f.close()
    return max([surface(t) for t in triangles])

print(solve())

Any idea why this isn't working?

suma=0
def area(x):
    p=list(int(i) for i in x)
    return 0.5*abs(p[0]*(p[3]-p[5])+p[2]*(p[5]-p[1])+p[4]*(p[1]-p[3]))
with open('TrianglePoints.txt','r') as f:
    for word in f:
        suma+=area(word.strip('\n'))
print(suma) #Returns 679.5

@Agnishom Chattopadhyay @Aditya Raut @Brock Brown

Pranjal Jain - 5 years, 9 months ago

We are looking for the maximum area not the sum.

Abdelhamid Saadi - 5 years, 9 months ago

Oh my bad! Why don't I read questions properly.

Pranjal Jain - 5 years, 9 months ago

Mark Mottian
Aug 1, 2015

My Java Solution:

import java.io.File;
import java.util.Scanner;


public class TriangleAreas {
        public static void main (String args []){
        try{
                        //read in the file
        Scanner file = new Scanner (new File ("TrianglePoints.txt")); 

            double maxArea = 0;
            while (file.hasNext()){
                              //read in each line of the file
              String line = file.nextLine(); 

                //find the x and y value for first co-ordinate
                int x1 = Integer.parseInt(line.charAt(0)+"");
                int y1 = Integer.parseInt(line.charAt(1)+"");

                //find the x and y value for second co-ordinate
                int x2 = Integer.parseInt(line.charAt(2)+"");
                int y2 = Integer.parseInt(line.charAt(3)+"");

                //find the x and y value for third co-ordinate
                int x3 = Integer.parseInt(line.charAt(4)+"");
                int y3 = Integer.parseInt(line.charAt(5)+"");

                //use the distance formula to get side lengths
                double length1 = 
             Math.sqrt(Math.pow((x1-x2), 2) + Math.pow((y1-y2), 2));
                 double length2 = 
             Math.sqrt(Math.pow((x3-x2), 2) + Math.pow((y3-y2), 2));
                double length3 = 
             Math.sqrt(Math.pow((x3-x1), 2) + Math.pow((y3-y1), 2));

            //use Heron's formula to calculate area
            double s = (length1+length2+length3)/(2.0);
            double area = 
                   Math.sqrt((s*(s-length1)*(s-length2)*(s-length3)));


            if (area > maxArea){ 
                maxArea = area;
            }
        }
        System.out.printf("%.1f",maxArea);
    }catch (Exception e){
        System.out.println(e);
    }
}

}

The program returns 23.5 as the answer

Nice problem! I found it easier to put it in Excel, get the individual digits, and use the matrix area formula below.

If your triangle has vertices $(a,b),(c,d),(e,f)$ then the area of the triangle is the absolute value of $\frac{ \left| \begin{array}{ccc} a & b & 1 \\ c & d & 1 \\ e & f & 1 \end{array} \right|}{2}$

Trevor B. - 5 years, 10 months ago

Did nearly the same thing, just used the expanded formula. If the points are labeled $(A_x,A_y)$ , $(B_x, B_y)$ , and $(C_x, C_y)$ :

$Area = \left|{\frac{A_x(B_y-C_y)+B_x(C_y-A_y)+C_x(A_y-B_y)}{2}}\right|$

The maximum comes from the triangle at the points $(7,8)$ , $(1,3)$ , $(8,1)$ .

Garrett Clarke - 5 years, 10 months ago

Geometry Meets Computer Science

The answer is 23.5.

7 solutions

0 pending reports