Ice cream on the side

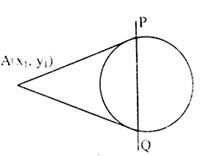
The point $P(6,8)$ is a distance of $10$ from the origin, so it will be the same if we just look at the tangents through the point $S(10,0)$ .

The area of the triangle as described will then be $A = y(10 - x)$ , where $(x,y)$ is the (upper) point of tangency. Now for the circle, the line of tangency to any point $(x,y)$ on the circle will have slope $-\dfrac{x}{y}$ . We thus will require that the line joining $S$ and $(x,y)$ have the same slope as the tangent line. This will be the case when

$\dfrac{-y}{10 - x} = -\dfrac{x}{y} \Longrightarrow y^{2} = x(10 - x) \Longrightarrow y = \sqrt{x(10 - x)}$ ,

as we are focusing on the point of tangency in the first quadrant. This gives us an expression for $A$ in terms of one variable, namely

$A(x) = \sqrt{x}(10 - x)^{\frac{3}{2}}$ .

Differentiating and setting equal to zero, we have

$A'(x) = \dfrac{1}{2\sqrt{x}}(10 - x)^{\frac{3}{2}} - \dfrac{3}{2}\sqrt{x}\sqrt{10 - x} = \dfrac{\sqrt{10 - x}}{2\sqrt{x}}(10 - 4x) = 0$ .

Now clearly $x \ne 10$ , so we are left with $10 - 4x = 0 \Longrightarrow x = \dfrac{5}{2}$ .

This gives us a value for $y$ of

$\sqrt{25 - \dfrac{25}{4}} = \dfrac{5}{2}\sqrt{3}$ ,

which in turn gives us a value for $r$ of

$\sqrt{\dfrac{25}{4} + \dfrac{25}{4}*3} = \sqrt{25} = \boxed{5}$ .

I used AM-GM $\displaystyle{3A^{ 2 }\left( x \right) =3x({ 10-x })^{ 3 }=3x({ 10-x })({ 10-x })({ 10-x })}$ Now Using Conditions of AM-GM inequality $\displaystyle{x\in (0,10)\\ 3x,({ 10-x }),({ 10-x }),({ 10-x })\longrightarrow AM-GM\\ AM=\cfrac { 30 }{ 4 } =constant\quad \\ 3x=10-x\quad \quad (\ GM\quad is\quad max\quad then\quad numbers\quad are\quad equal)\\ \Rightarrow \boxed { x=\cfrac { 5 }{ 2 } } }$